Nelle sezioni seguenti, illustreremo la programmazione dei vincoli (CP) in base a combinatorio basato sul gioco degli scacchi. A scacchi una regina può attaccare orizzontalmente, verticalmente e diagonalmente. Il problema delle N-queens chiede:
Come è possibile posizionare N regine su una scacchiera NxN per evitare che due di loro attaccano tra loro?
Di seguito è riportata una possibile soluzione al problema delle N-queen per N = 4.
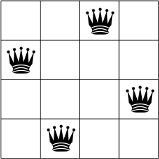
Non esistono due regine sulla stessa riga, colonna o diagonale.
Tieni presente che questo non è un problema di ottimizzazione: vogliamo trovare tutto il possibile di alta qualità, piuttosto che una sola soluzione ottimale, il che la rende un candidato naturale per la programmazione di vincoli. Le seguenti sezioni descrivono l'approccio CP al problema delle N-queens. presentare programmi che lo risolvano utilizzando sia il risolutore CP-SAT sia il CP originale risolutore.
Approccio CP al problema delle N-queens
Un risolutore CP lavora provando sistematicamente tutti le possibili assegnazioni di valori alle variabili in un problema, per trovare soluzioni realizzabili. Nel problema delle 4 regine, il risolutore parte dall'estrema sinistra. colonna e posiziona in successione una regina in ogni colonna, in una posizione non attaccati da regine precedentemente posizionate.
Propagazione e backtracking
Ci sono due elementi chiave in una ricerca di vincolo di programmazione:
- Propagazione: ogni volta che il risolutore assegna un valore a una variabile, i vincoli aggiungono restrizioni sui possibili valori degli come la codifica one-hot delle variabili categoriche. Queste restrizioni si propagano ad assegnazioni di variabili future. Ad esempio, nel problema delle 4 regine, ogni volta che il risolutore posiziona una regina, non può posizionare altre regine sulla fila e sulle diagonali in cui si trova la regina corrente. La propagazione può velocizzare significativamente la ricerca riducendo l'insieme di e i valori delle variabili che il risolutore deve esplorare.
- Il backtracking si verifica quando il risolutore non può assegnare un valore al successivo a causa dei vincoli, oppure trova una soluzione. In entrambi i casi, risolutore torna alla fase precedente e cambia il valore della variabile quella fase a un valore che non è stato ancora provato. Nell'esempio delle 4 regine, Ciò significa spostare una regina in un nuovo quadrato nella colonna corrente.
Ora vedremo come la programmazione dei vincoli utilizza la propagazione e il backtracking risolvere il problema delle 4 regine.
Supponiamo che il risolutore inizi posizionando arbitrariamente una regina in alto a sinistra. nell'angolo superiore della pagina. Questa è una specie di ipotesi: potresti scoprire che non c'è soluzione esiste con una regina nell'angolo superiore sinistro.
Partendo da questa ipotesi, quali vincoli possiamo propagare? Un vincolo è che ci può essere solo una regina in una colonna (le X grigie sotto) e un'altra il vincolo vieta due regine sulla stessa diagonale (le X rosse sotto).
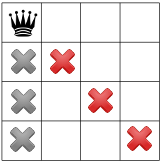
Il nostro terzo vincolo vieta le regine nella stessa riga:
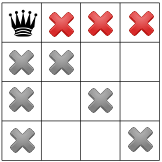
I nostri vincoli si sono propagati, possiamo testare un'altra ipotesi e porre una seconda regina su uno dei quadrati rimanenti disponibili. Il nostro risolutore potrebbe decidere per posizionare al suo interno il primo quadrato disponibile nella seconda colonna:
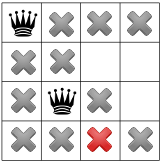
Dopo aver propagato il vincolo diagonale, possiamo vedere che non lascia quadrati disponibili nella terza colonna o nell'ultima riga:
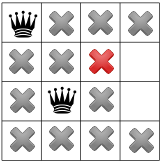
In questa fase non è possibile trovare soluzioni, dobbiamo fare un passo indietro. Un'opzione è perché il risolutore scelga l'altro quadrato disponibile nella seconda colonna. Tuttavia, la propagazione del vincolo forza quindi una regina nella seconda riga del terza colonna, senza lasciare spazi validi per la quarta regina:

Quindi il risolutore deve tornare indietro, questa volta posizionamento della prima regina. Abbiamo dimostrato che non c'è soluzione per le regine occuperà un quadrato d'angolo.
Poiché non ci possono essere regine nell'angolo, il risolutore sposta la prima regina verso il basso per uno e si propaga, lasciando un solo posto alla seconda regina:
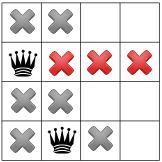
La propagazione di nuovo rivela un solo posto alla terza regina:
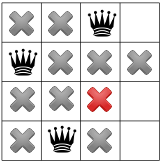
E per la quarta e ultima regina:

Abbiamo la nostra prima soluzione! Se abbiamo chiesto al nostro risolutore di fermarsi dopo aver trovato con la prima soluzione. Altrimenti, tornerà indietro posiziona la prima regina nella terza riga della prima colonna.
Soluzione che utilizza CP-SAT
Il problema delle N-queens è ideale per la programmazione di vincoli. In questo esamineremo un breve programma Python che utilizza il risolutore CP-SAT trovare tutte le soluzioni al problema.
Importa le librerie
Il codice seguente importa la libreria richiesta.
Python
import sys import time from ortools.sat.python import cp_model
C++
#include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h"
Java
import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr;
C#
using System; using Google.OrTools.Sat;
Dichiara il modello
Il seguente codice dichiara il modello CP-SAT.
Python
model = cp_model.CpModel()
C++
CpModelBuilder cp_model;
Java
CpModel model = new CpModel();
C#
CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
Crea le variabili
Il risolutore crea le variabili per il problema sotto forma di array denominato queens.
Python
# There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]
C++
// There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); }
Java
int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); }
C#
int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); }
Supponiamo che queens[j] sia il numero di riga della regina nella colonna j.
In altre parole, queens[j] = i significa che c'è una regina nella riga i e nella colonna j.
crea i vincoli
Ecco il codice che crea i vincoli per il problema.
Python
# All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size))
C++
// The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2);
Java
// All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2);
C#
// All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2);
Il codice utilizza il metodo AddAllDifferent, che richiede tutti gli elementi di un
in un array di variabili.
Vediamo in che modo questi vincoli garantiscono le tre condizioni delle N-queen problema (regine su righe, colonne e diagonali diverse).
Non esistono due regine sulla stessa riga
L'applicazione del metodo AllDifferent del risolutore a queens forza i valori di
queens[j] sia diverso per ogni j, il che significa che tutte le regine devono trovarsi
in righe diverse.
Non esistono due regine nella stessa colonna
Questo vincolo è implicito nella definizione di queens.
Poiché non esistono due elementi di queens possono avere lo stesso indice, non possono essere
nella stessa colonna.
Non esistono due regine sulla stessa diagonale
Il vincolo diagonale è un po' più complesso dei vincoli di riga e colonna. Innanzitutto, se due regine giacciono sulla stessa diagonale, una delle seguenti condizioni deve essere vero:
- Il numero di riga più il numero di colonna per ciascuna delle due regine sono uguali.
In altre parole,
queens(j) + jha lo stesso valore per due indici diversij. - Il numero di riga meno il numero di colonna per ciascuna delle due regine sono uguali.
In questo caso,
queens(j) - jha lo stesso valore per due diversi indicij.
Una di queste condizioni significa che le regine giacciono sulla stessa diagonale crescente ( va da sinistra a destra), mentre l'altra giace nella stessa direzione discendente in diagonale. Quale condizione corrisponde a crescente e quale a decrescente dipende dall'ordinamento di righe e colonne. Come indicato nel sezione precedente, l'ordinamento non influisce sull'insieme di soluzioni, proprio come le immagini.
Il vincolo diagonale è che i valori di queens(j) + j devono essere tutti
e i valori di queens(j) - j devono essere tutti diversi, per
j diversi.
Per applicare il metodo AddAllDifferent a queens(j) + j, abbiamo inserito le N istanze
della variabile, per j da 0 a N-1, in un array, diag1, come segue:
q1 = model.NewIntVar(0, 2 * board_size, 'diag1_%i' % i) diag1.append(q1) model.Add(q1 == queens[j] + j)
Quindi applichiamo AddAllDifferent a diag1.
model.AddAllDifferent(diag1)
Il vincolo per queens(j) - j viene creato in modo simile.
Crea una stampante della soluzione
Per stampare tutte le soluzioni al problema delle N-queens, devi superare un callback, chiamata stampante di soluzione, al risolutore CP-SAT. Il callback stampa ogni una nuova soluzione così come la trova il risolutore. Il codice seguente crea una soluzione stampante.
Python
class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print()
C++
int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; }));
Java
static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; }
C#
public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; }
Tieni presente che la stampante della soluzione deve essere scritta come classe Python, a causa del l'interfaccia Python al risolutore C++ sottostante.
Le soluzioni vengono stampate dalle righe seguenti nella stampante della soluzione.
for v in self.__variables: print('%s = %i' % (v, self.Value(v)), end = ' ')
In questo esempio, self.__variables è la variabile queens e ogni v
corrisponde a una delle otto voci di queens. Viene stampata una soluzione
il modulo seguente: x0 = queens(0) x1 = queens(1) ... x7 = queens(7) dove
xi è il numero di colonna della regina nella riga i.
La sezione successiva mostra un esempio di soluzione.
Chiamare il risolutore e visualizzare i risultati
Il seguente codice esegue il risolutore e mostra le soluzioni.
Python
solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer)
C++
// Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions;
Java
CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb);
C#
// Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb);
Il programma trova 92 soluzioni diverse per una scheda 8x8. Quesito numero uno in arrivo.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Solutions found: 92Puoi risolvere il problema per una bacheca di dimensioni diverse passando N come
dall'argomento della riga di comando. Ad esempio, se il programma si chiama queens,
python nqueens_sat.py 6 risolve il problema di una scheda 6x6.
L'intero programma
Ecco l'intero programma del programma N-queens.
Python
"""OR-Tools solution to the N-queens problem.""" import sys import time from ortools.sat.python import cp_model class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() def main(board_size: int) -> None: # Creates the solver. model = cp_model.CpModel() # Creates the variables. # There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size)) # Solve the model. solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer) # Statistics. print("\nStatistics") print(f" conflicts : {solver.num_conflicts}") print(f" branches : {solver.num_branches}") print(f" wall time : {solver.wall_time} s") print(f" solutions found: {solution_printer.solution_count}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h" namespace operations_research { namespace sat { void NQueensSat(const int board_size) { // Instantiate the solver. CpModelBuilder cp_model; // There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2); int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; })); // Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions; // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << CpSolverResponseStats(response); } } // namespace sat } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { if (!absl::SimpleAtoi(argv[1], &board_size)) { LOG(INFO) << "Cannot parse '" << argv[1] << "', using the default value of 8."; board_size = 8; } } operations_research::sat::NQueensSat(board_size); return EXIT_SUCCESS; }
Java
package com.google.ortools.sat.samples; import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr; /** OR-Tools solution to the N-queens problem. */ public final class NQueensSat { static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; } public static void main(String[] args) { Loader.loadNativeLibraries(); // Create the model. CpModel model = new CpModel(); int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2); // Create a solver and solve the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb); // Statistics. System.out.println("Statistics"); System.out.println(" conflicts : " + solver.numConflicts()); System.out.println(" branches : " + solver.numBranches()); System.out.println(" wall time : " + solver.wallTime() + " s"); System.out.println(" solutions : " + cb.getSolutionCount()); } private NQueensSat() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.Sat; public class NQueensSat { public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; } static void Main() { // Constraint programming engine CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
Soluzione che utilizza il risolutore CP originale
Le sezioni seguenti presentano un programma Python che risolve le N-queen utilizzando come un risolutore CP originale. (Tuttavia, ti consigliamo di utilizzare il risolutore CP-SAT più recente)
Importa le librerie
Il codice seguente importa la libreria richiesta.
Python
import sys from ortools.constraint_solver import pywrapcp
C++
#include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h"
Java
import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver;
C#
using System; using Google.OrTools.ConstraintSolver;
Dichiara il risolutore
Il seguente codice dichiara il risolutore CP originale.
Python
solver = pywrapcp.Solver("n-queens")
C++
Solver solver("N-Queens");
Java
Solver solver = new Solver("N-Queens");
C#
Solver solver = new Solver("N-Queens");
Crea le variabili
Il metodo IntVar del risolutore crea le variabili per il problema sotto forma di array
denominato queens.
Python
# The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]
C++
std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); }
Java
int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); }
C#
const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); }
Per qualsiasi soluzione, queens[j] = i significa che nella colonna j e nella riga è presente una regina
i.
crea i vincoli
Ecco il codice che crea i vincoli per il problema.
Python
# All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))
C++
// The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2));
Java
// All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2));
C#
// All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent());
Questi vincoli garantiscono le tre condizioni necessarie per il problema delle N-queens ( regine su righe, colonne e diagonali diverse).
Non esistono due regine sulla stessa riga
L'applicazione del metodo AllDifferent del risolutore a queens forza i valori di
queens[j] sia diverso per ogni j, il che significa che tutte le regine devono trovarsi
in righe diverse.
Non esistono due regine nella stessa colonna
Questo vincolo è implicito nella definizione di queens.
Poiché non esistono due elementi di queens possono avere lo stesso indice, non possono essere
nella stessa colonna.
Non esistono due regine sulla stessa diagonale
Il vincolo diagonale è un po' più complesso dei vincoli di riga e colonna. Innanzitutto, se due regine giacciono sulla stessa diagonale, deve essere vera una delle seguenti condizioni:
- Se la diagonale è decrescente (da sinistra a destra), il numero di riga più
il numero di colonna per ciascuna delle due regine è uguale. Quindi
queens(i) + iha lo stesso valore per due diversi indicii. - Se la diagonale è crescente, il numero di riga meno il numero di colonna per ogni
delle due regine sono uguali. In questo caso,
queens(i) - iha lo stesso valore per due diversi indicii.
Il vincolo diagonale è che i valori di queens(i) + i devono essere tutti
e allo stesso modo i valori di queens(i) - i devono essere tutti diversi,
i diversi.
Il codice riportato sopra aggiunge questo vincolo applicando il metodo
AllDifferent
in queens[j] + j e queens[j] - j, per ogni i.
Aggiungere il generatore di decisioni
Il passaggio successivo consiste nel creare un generatore di decisioni, che imposta la strategia di ricerca per risolvere il problema. La strategia di ricerca può avere un grande impatto sui tempi di ricerca, a causa della propagazione dei vincoli, che riduce il numero di valori variabili che il risolutore deve esplorare. Ne avete già visto un esempio nel Esempio di 4 regine.
Il codice seguente crea un generatore di decisioni utilizzando
Phase
.
Python
db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
C++
DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);
Java
// Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
C#
// Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
Consulta Generatore di decisioni per maggiori dettagli sulla
argomenti di input al metodo Phase.
Come funziona il generatore di decisioni nell'esempio delle 4 regine
Vediamo in che modo il generatore di decisioni dirige la ricerca
Esempio di 4 regine.
Il risolutore inizia con queens[0], la prima variabile dell'array, come indicato
di CHOOSE_FIRST_UNBOUND. Il risolutore assegna quindi queens[0]
non ancora provato, che in questa fase è 0, come indicato
ASSIGN_MIN_VALUE. La prima regina viene posizionata nell'angolo superiore sinistro della
.
Successivamente, il risolutore seleziona queens[1], che ora è la prima variabile non associata in
queens. Dopo la propagazione dei vincoli, esistono due righe possibili per un
regina nella colonna 1: riga 2 o riga 3. L'opzione ASSIGN_MIN_VALUE indirizza
risolutore per assegnare queens[1] = 2. Se invece imposti IntValueStrategy su
ASSIGN_MAX_VALUE, il risolutore assegnerà queens[1] = 3.)
Puoi verificare che il resto della ricerca segua le stesse regole.
Chiamare il risolutore e visualizzare i risultati
Il seguente codice esegue il risolutore e mostra la soluzione.
Python
# Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch()
C++
// Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch();
Java
int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch();
C#
// Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch();
Ecco la prima soluzione trovata dal programma per una scheda 8x8.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Statistics
failures: 304
branches: 790
wall time: 5 ms
Solutions found: 92Puoi risolvere il problema per una bacheca di dimensioni diverse passando N come
dall'argomento della riga di comando. Ad esempio, python nqueens_cp.py 6 risolve il problema
per una tavola 6x6.
L'intero programma
Di seguito è mostrato il programma completo.
Python
"""OR-Tools solution to the N-queens problem.""" import sys from ortools.constraint_solver import pywrapcp def main(board_size): # Creates the solver. solver = pywrapcp.Solver("n-queens") # Creates the variables. # The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)])) db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE) # Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch() # Statistics. print("\nStatistics") print(f" failures: {solver.Failures()}") print(f" branches: {solver.Branches()}") print(f" wall time: {solver.WallTime()} ms") print(f" Solutions found: {num_solutions}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h" namespace operations_research { void NQueensCp(const int board_size) { // Instantiate the solver. Solver solver("N-Queens"); std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2)); DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch(); // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << " failures: " << solver.failures(); LOG(INFO) << " branches: " << solver.branches(); LOG(INFO) << " wall time: " << solver.wall_time() << " ms"; LOG(INFO) << " Solutions found: " << num_solutions; } } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { board_size = std::atoi(argv[1]); } operations_research::NQueensCp(board_size); return EXIT_SUCCESS; }
Java
// OR-Tools solution to the N-queens problem. package com.google.ortools.constraintsolver.samples; import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver; /** N-Queens Problem. */ public final class NQueensCp { public static void main(String[] args) { Loader.loadNativeLibraries(); // Instantiate the solver. Solver solver = new Solver("N-Queens"); int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2)); // Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch(); // Statistics. System.out.println("Statistics"); System.out.println(" failures: " + solver.failures()); System.out.println(" branches: " + solver.branches()); System.out.println(" wall time: " + solver.wallTime() + "ms"); System.out.println(" Solutions found: " + solutionCount); } private NQueensCp() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.ConstraintSolver; public class NQueensCp { public static void Main(String[] args) { // Instantiate the solver. Solver solver = new Solver("N-Queens"); const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent()); // Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch(); // Statistics. Console.WriteLine("Statistics"); Console.WriteLine($" failures: {solver.Failures()}"); Console.WriteLine($" branches: {solver.Branches()}"); Console.WriteLine($" wall time: {solver.WallTime()} ms"); Console.WriteLine($" Solutions found: {SolutionCount}"); } }
Numero di soluzioni
Il numero di soluzioni aumenta in modo esponenziale con le dimensioni del consiglio di amministrazione:
| Dimensioni della scheda | Soluzioni | Tempo per trovare tutte le soluzioni (ms) |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 2 | 0 |
| 5 | 10 | 0 |
| 6 | 4 | 0 |
| 7 | 40 | 3 |
| 8 | 92 | 9 |
| 9 | 352 | 35 |
| 10 | 724 | 95 |
| 11 | 2680 | 378 |
| 12 | 14200 | 2198 |
| 13 | 73712 | 11628 |
| 14 | 365596 | 62427 |
| 15 | 2279184 | 410701 |
Molte soluzioni sono solo rotazioni di altre e una tecnica chiamata simmetria che consente di ridurre la quantità di calcolo necessaria. Non utilizziamo che qui: la soluzione illustrata sopra non è concepita per essere veloce, solo semplice. Naturalmente, potremmo renderlo molto più veloce se volessimo trovare una sola soluzione invece di tutte: non più di pochi millisecondi per schede di dimensioni fino a 50.
