다음 섹션에서는 제약 조건 프로그래밍 (CP)을 조합 문제를 일으킬 수 있습니다. 체스에서는 여왕이 공격할 수 있다 가로, 세로, 대각선 방향의 조합으로 구성됩니다. N-퀸즈 문제는 다음과 같이 묻습니다.
두 마리의 퀸을 NxN 체스판에 올라 두 명이 공격하지 못하도록 하려면 어떻게 해야 할까요? 어떻게 해야 할까요?
아래에서는 N = 4인 N-퀸 문제에 대한 한 가지 가능한 해결책을 확인할 수 있습니다.
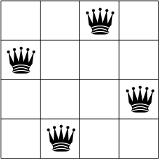
같은 행, 기둥 또는 대각선 위에 두 개의 퀸이 없습니다.
이는 최적화 문제가 아닙니다. 가능한 한 하나의 최적 솔루션이 아닌 당연한 제약 조건 프로그래밍에 사용할 수 있습니다. 다음 섹션에서는 N-퀸 문제에 대한 CP 접근 방식을 설명하고 CP-SAT 솔버와 원래 CP를 모두 사용하여 이를 해결하는 프로그램을 제시 문제 해결사의 약어입니다.
N-퀸 문제에 대한 CP 접근방식
CP 솔버는 모든 문제를 체계적으로 시도하여 문제의 변수에 값을 할당할 수 있는 살펴봤습니다 여왕 4개 문제에서 문제 해결사는 가장 왼쪽부터 시작합니다. 열을 배치하고 다음 위치에 연속적으로 각 열에 한 퀸을 배치합니다. 이전에 배치된 여왕의 공격을 받지 않게 됩니다.
전파 및 역추적
제약조건 프로그래밍 검색에는 두 가지 핵심 요소가 있습니다.
- 전파 — 문제 해결사가 변수에 값을 할당할 때마다 제약 조건은 할당되지 않은 값의 가능한 값에 대한 제한을 추가합니다. 변수로 사용할 수 있습니다. 이러한 제한은 향후 변수 할당에 전파됩니다. 예를 들어, 여왕 4개 문제에서 문제 해결사가 퀸을 배치할 때마다 행에 다른 퀸을 배치할 수 없습니다. 현재 퀸이 켜져 있는 대각선입니다. 이렇게 전파하면 참조 집합 수를 줄임으로써 검색 속도를 크게 문제 해결자가 탐색해야 하는 변수 값입니다.
- 백추적은 문제 해결사가 다음 작업에 값을 할당할 수 없을 때 발생합니다. 변수를 호출하거나 해결책을 찾습니다. 두 경우 모두 솔버가 이전 단계로 백트래킹하고 이전 단계로 값을 새 값으로 전달할 수 있습니다. 4-퀸즈 예에서 이는 여왕을 현재 열의 새 정사각형으로 이동하는 것을 의미합니다.
다음으로 제약조건 프로그래밍이 어떻게 전파 및 역추적을 사용하여 4 여왕 문제를 해결합니다.
문제 해결사가 왼쪽 상단에 임의로 여왕을 배치한다고 가정해 보겠습니다. 있습니다. 일종의 가설이죠. 어떤 솔루션도 왼쪽 상단에 여왕이 있습니다.
이 가설을 고려할 때 어떤 제약 조건을 전파할 수 있을까요? 한 가지 제약 조건은 한 열에 하나의 퀸만 있을 수 있습니다 (아래 회색 X 표시). 제약 조건은 동일한 대각선에서 두 개의 퀸을 금지합니다 (아래 빨간색 X 표시).
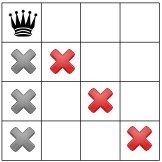
세 번째 제약조건은 동일한 행에서 퀸을 금지합니다.
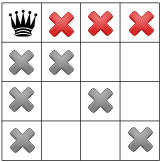
제약 조건이 전파되면 다른 가설을 테스트하고 두 번째 퀸을 정사각형으로 반환합니다. 문제 해결사는 두 번째 열의 사용 가능한 첫 번째 정사각형을 배치합니다.
대각선 제약 조건을 전파한 후에는 세 번째 열 또는 마지막 행에 사용할 수 있는 정사각형:
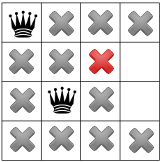
이 단계에서 가능한 해결책이 없다면 이전으로 되돌아가야 합니다. 한 가지 옵션은 문제 해결사가 두 번째 열에서 사용 가능한 다른 정사각형을 선택합니다. 그러나 제약 조건 전파는 퀸을 세 번째 열, 네 번째 여왕을 위한 유효한 자리가 남아 있지 않습니다.

그래서 문제 해결사는 다시 처음부터 다시 추적해야 하는데, 이번에는 첫 번째 여왕의 좌석을 차지했습니다. 이제 우리는 여왕을 해결할 해결책이 없다고 모서리 정사각형을 차지하게 됩니다.
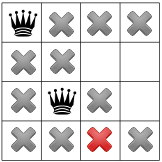
구석에 여왕이 없을 수 있기 때문에 문제 해결사는 첫 번째 여왕을 아래로 움직입니다. 하나씩 전파되어 두 번째 여왕의 자리 하나만 남깁니다.
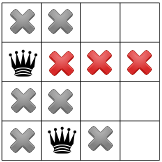
다시 한번 해보면 세 번째 여왕의 자리가 한 곳밖에 남았네요.
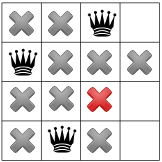
네 번째이자 마지막 여왕:

첫 번째 해결책이 있습니다! 문제 해결사가 첫 번째 솔루션은 여기서 끝납니다 그렇지 않으면 다시 이전하여 첫 번째 열의 세 번째 행에 첫 번째 여왕을 배치합니다.
CP-SAT를 사용한 솔루션
N-퀸 문제는 제약 조건 프로그래밍에 이상적입니다. 이 섹션에서는 CP-SAT 솔버를 사용하여 문제를 해결하는 간단한 Python 프로그램을 살펴보겠습니다. 문제에 대한 모든 솔루션을 찾을 수 있습니다
라이브러리 가져오기
다음 코드는 필요한 라이브러리를 가져옵니다.
Python
import sys import time from ortools.sat.python import cp_model
C++
#include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h"
자바
import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr;
C#
using System; using Google.OrTools.Sat;
모델 선언
다음 코드는 CP-SAT 모델을 선언합니다.
Python
model = cp_model.CpModel()
C++
CpModelBuilder cp_model;
자바
CpModel model = new CpModel();
C#
CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
변수 만들기
문제 해결 도구는 queens이라는 배열로 문제의 변수를 만듭니다.
Python
# There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]
C++
// There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); }
자바
int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); }
C#
int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); }
여기서는 queens[j]가 j 열에 있는 퀸의 행 번호라고 가정합니다.
즉, queens[j] = i은 i행과 j열에 퀸이 있음을 의미합니다.
제약조건 만들기
다음은 문제의 제약 조건을 생성하는 코드입니다.
Python
# All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size))
C++
// The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2);
자바
// All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2);
C#
// All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2);
이 코드는 AddAllDifferent 메서드를 사용합니다. 이 메서드에는
변수 배열이 달라야 합니다.
이러한 제약 조건이 어떻게 N-퀸의 세 가지 조건을 보장하는지 여왕이 여러 행, 열, 대각선에 있음).
같은 줄에 있는 두 퀸은 없다
솔버의 AllDifferent 메서드를 queens에 적용하면
queens[j]가 j마다 달라야 합니다. 즉, 모든 퀸이
지정할 수 있습니다.
같은 열에 두 퀸은 없다
이 제약조건은 queens 정의에 암시적입니다.
queens의 두 요소의 색인이 같을 수 없으므로 두 개의 퀸이 있을 수 없습니다.
을 입력합니다.
같은 대각선 위에 있는 두 여왕은 없다
대각선 제약 조건은 행 및 열 제약 조건보다 약간 까다롭습니다. 첫째, 두 마리의 여왕이 같은 대각선 위에 놓인 경우 다음 조건 중 하나 가 true여야 합니다.
- 두 퀸의 행 번호와 열 번호를 더한 값은 같습니다.
즉, 두 개의 서로 다른 색인에 대해
queens(j) + j의 값이 같습니다.j입니다. - 두 퀸의 행 번호에서 열 번호를 뺀 값이 동일합니다.
이 경우
queens(j) - j은 두 개의 다른 색인j에 대해 동일한 값을 갖습니다.
이러한 조건 중 하나는 여왕이 동일한 오름차순 대각선 ( 다른 하나는 동일한 내림차순에 놓인다는 것을 의미합니다. 대각선. 오름차순에 해당하는 조건과 내림차순에 해당하는 조건 행과 열의 순서를 지정하는 방법에 따라 다릅니다. 'API 약관'의 이전 섹션에서 설명하자면, 순서는 시각화하는 방법에 따라 달라집니다
따라서 대각선 제약 조건은 queens(j) + j의 값이 모두
다르고 queens(j) - j의 값이 모두 달라야 합니다.
다른 j.
AddAllDifferent 메서드를 queens(j) + j에 적용하기 위해 N개의 인스턴스를 배치합니다.
0에서 N-1까지의 j에 대한 변수의 값을 다음과 같이 diag1 배열로 변환합니다.
q1 = model.NewIntVar(0, 2 * board_size, 'diag1_%i' % i) diag1.append(q1) model.Add(q1 == queens[j] + j)
그런 다음 AddAllDifferent를 diag1에 적용합니다.
model.AddAllDifferent(diag1)
queens(j) - j의 제약 조건은 비슷하게 생성됩니다.
솔루션 프린터 만들기
N-퀸 문제에 모든 해답을 출력하려면 콜백을 전달해야 합니다. 솔루션 프린터라고 하는 CP-SAT 솔버에 연결합니다. 콜백은 각 새 솔루션을 찾아낼 수 있습니다. 다음 코드는 솔루션을 생성합니다. 표시됩니다.
Python
class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print()
C++
int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; }));
자바
static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; }
C#
public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; }
솔루션 프린터는 기본 C++ 솔버에 대한 Python 인터페이스입니다.
솔루션은 솔루션 프린터에서 다음 줄로 인쇄됩니다.
for v in self.__variables: print('%s = %i' % (v, self.Value(v)), end = ' ')
이 예에서 self.__variables는 queens 변수이며 각 v는
queens의 8개 항목 중 하나에 해당합니다. 이렇게 하면
다음 형식이 필요합니다. x0 = queens(0) x1 = queens(1) ... x7 = queens(7) 각 항목의 의미는 다음과 같습니다.
xi는 i행에 있는 퀸의 열 번호입니다.
다음 섹션에서는 솔루션의 예를 보여줍니다.
솔버를 호출하고 결과 표시
다음 코드는 솔버를 실행하고 해답을 표시합니다.
Python
solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer)
C++
// Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions;
자바
CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb);
C#
// Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb);
이 프로그램은 8x8 보드에 맞는 92개의 서로 다른 솔루션을 찾아 냅니다. 첫 번째 질문은 다음과 같습니다.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Solutions found: 92N을
명령줄 인수를 사용합니다. 예를 들어 프로그램 이름이 queens인 경우
python nqueens_sat.py 6는 6x6 보드의 문제를 해결합니다.
전체 프로그램
다음은 N-퀸스 프로그램의 전체 프로그램입니다.
Python
"""OR-Tools solution to the N-queens problem.""" import sys import time from ortools.sat.python import cp_model class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() def main(board_size: int) -> None: # Creates the solver. model = cp_model.CpModel() # Creates the variables. # There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size)) # Solve the model. solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer) # Statistics. print("\nStatistics") print(f" conflicts : {solver.num_conflicts}") print(f" branches : {solver.num_branches}") print(f" wall time : {solver.wall_time} s") print(f" solutions found: {solution_printer.solution_count}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h" namespace operations_research { namespace sat { void NQueensSat(const int board_size) { // Instantiate the solver. CpModelBuilder cp_model; // There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2); int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; })); // Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions; // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << CpSolverResponseStats(response); } } // namespace sat } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { if (!absl::SimpleAtoi(argv[1], &board_size)) { LOG(INFO) << "Cannot parse '" << argv[1] << "', using the default value of 8."; board_size = 8; } } operations_research::sat::NQueensSat(board_size); return EXIT_SUCCESS; }
자바
package com.google.ortools.sat.samples; import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr; /** OR-Tools solution to the N-queens problem. */ public final class NQueensSat { static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; } public static void main(String[] args) { Loader.loadNativeLibraries(); // Create the model. CpModel model = new CpModel(); int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2); // Create a solver and solve the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb); // Statistics. System.out.println("Statistics"); System.out.println(" conflicts : " + solver.numConflicts()); System.out.println(" branches : " + solver.numBranches()); System.out.println(" wall time : " + solver.wallTime() + " s"); System.out.println(" solutions : " + cb.getSolutionCount()); } private NQueensSat() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.Sat; public class NQueensSat { public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; } static void Main() { // Constraint programming engine CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
원래 CP 솔버를 사용한 솔루션
다음 섹션에서는 원래 CP 문제 해결사입니다. 하지만 최신 CP-SAT 솔버를 사용하는 것이 좋습니다.
라이브러리 가져오기
다음 코드는 필요한 라이브러리를 가져옵니다.
Python
import sys from ortools.constraint_solver import pywrapcp
C++
#include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h"
자바
import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver;
C#
using System; using Google.OrTools.ConstraintSolver;
문제 해결사 선언
다음 코드는 원래 CP 솔버를 선언합니다.
Python
solver = pywrapcp.Solver("n-queens")
C++
Solver solver("N-Queens");
자바
Solver solver = new Solver("N-Queens");
C#
Solver solver = new Solver("N-Queens");
변수 만들기
문제 해결사의 IntVar 메서드는 문제의 변수를 배열로 생성
이름이 queens입니다.
Python
# The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]
C++
std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); }
자바
int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); }
C#
const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); }
모든 솔루션에서 queens[j] = i은 j열과 행에 퀸이 있음을 의미합니다.
i입니다.
제약조건 만들기
다음은 문제의 제약 조건을 생성하는 코드입니다.
Python
# All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))
C++
// The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2));
자바
// All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2));
C#
// All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent());
이러한 제약 조건은 N-퀸 문제 ( 여왕이 여러 행, 열, 대각선에 있음).
같은 줄에 있는 두 퀸은 없다
솔버의 AllDifferent 메서드를 queens에 적용하면
queens[j]가 j마다 달라야 합니다. 즉, 모든 퀸이
지정할 수 있습니다.
같은 열에 두 퀸은 없다
이 제약조건은 queens 정의에 암시적입니다.
queens의 두 요소의 색인이 같을 수 없으므로 두 개의 퀸이 있을 수 없습니다.
을 입력합니다.
같은 대각선 위에 있는 두 여왕은 없다
대각선 제약 조건은 행 및 열 제약 조건보다 약간 까다롭습니다. 첫째, 두 마리의 여왕이 같은 대각선 위에 놓인 경우 다음 중 하나에 해당해야 합니다.
- 대각선이 내림차순 (왼쪽에서 오른쪽으로)인 경우 행 번호와
두 퀸의 각각 열 번호가 같다고 가정해 보겠습니다. 따라서
queens(i) + i는 두 개의 다른 색인에 대한 동일한 값i. - 대각선이 오름차순이면 행 번호에서 각 열의 열 번호를 뺀 값입니다.
2개의 퀸이 같다는 것입니다. 이 경우
queens(i) - i의 값이 동일합니다. 두 개의 다른 색인i에 대한 결과입니다.
따라서 대각선 제약 조건은 queens(i) + i의 값이 모두
마찬가지로 queens(i) - i의 값도 모두 달라야 합니다.
다른 i.
위의 코드는
AllDifferent 드림
각 i에 대해 queens[j] + j 및 queens[j] - j 메서드를 호출합니다.
의사 결정 빌더 추가
다음 단계는 검색 전략을 설정하는 의사결정 도구를 만드는 것입니다. 확인할 수 있습니다 검색 전략은 검색 시간, 제약조건이 전파되어 변수 값의 개수를 줄여줍니다. 문제 해결사는 탐색해야 합니다 이와 관련된 예는 퀸 4개 예
다음 코드는 솔버의
Phase 드림
메서드를 사용하여 축소하도록 요청합니다.
Python
db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
C++
DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);
자바
// Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
C#
// Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
자세한 내용은 결정 빌더를 참고하세요.
입력 인수를 Phase 메서드에 추가합니다.
여왕 4개 사례에서 의사결정권자의 작동 방식
의사 결정 빌더가
퀸 4개 예
문제 해결사는 지시에 따라 배열의 첫 번째 변수인 queens[0]로 시작합니다.
작성자: CHOOSE_FIRST_UNBOUND 그런 다음 문제 해결사는 queens[0]에 가장 작은 값을 할당합니다.
0으로 설정합니다. 이 단계에서는 아직 시도되지 않은
ASSIGN_MIN_VALUE입니다. 그러면 첫 번째 퀸이
있습니다.
다음으로, 솔버는 queens[1]를 선택합니다. 이는 이제
queens입니다. 제약조건을 전파한 후에는 단일 열에 대해 가능한 두 개의 행이
퀸: 2행 또는 3행. ASSIGN_MIN_VALUE 옵션은
솔버가 queens[1] = 2를 할당합니다. (대신 IntValueStrategy를 다음과 같이 설정합니다.
ASSIGN_MAX_VALUE이면 문제 해결사는 queens[1] = 3를 할당합니다.)
검색의 나머지 부분이 동일한 규칙을 따르는지 확인할 수 있습니다.
솔버를 호출하고 결과 표시
다음 코드는 솔버를 실행하고 솔루션을 표시합니다.
Python
# Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch()
C++
// Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch();
자바
int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch();
C#
// Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch();
다음은 8x8 보드에 대해 프로그램이 발견한 첫 번째 솔루션입니다.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Statistics
failures: 304
branches: 790
wall time: 5 ms
Solutions found: 92N을
명령줄 인수를 사용합니다. 예를 들어 python nqueens_cp.py 6는 문제를 해결합니다.
6x6 보드용입니다.
전체 프로그램
전체 프로그램은 다음과 같습니다.
Python
"""OR-Tools solution to the N-queens problem.""" import sys from ortools.constraint_solver import pywrapcp def main(board_size): # Creates the solver. solver = pywrapcp.Solver("n-queens") # Creates the variables. # The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)])) db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE) # Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch() # Statistics. print("\nStatistics") print(f" failures: {solver.Failures()}") print(f" branches: {solver.Branches()}") print(f" wall time: {solver.WallTime()} ms") print(f" Solutions found: {num_solutions}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h" namespace operations_research { void NQueensCp(const int board_size) { // Instantiate the solver. Solver solver("N-Queens"); std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2)); DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch(); // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << " failures: " << solver.failures(); LOG(INFO) << " branches: " << solver.branches(); LOG(INFO) << " wall time: " << solver.wall_time() << " ms"; LOG(INFO) << " Solutions found: " << num_solutions; } } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { board_size = std::atoi(argv[1]); } operations_research::NQueensCp(board_size); return EXIT_SUCCESS; }
자바
// OR-Tools solution to the N-queens problem. package com.google.ortools.constraintsolver.samples; import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver; /** N-Queens Problem. */ public final class NQueensCp { public static void main(String[] args) { Loader.loadNativeLibraries(); // Instantiate the solver. Solver solver = new Solver("N-Queens"); int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2)); // Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch(); // Statistics. System.out.println("Statistics"); System.out.println(" failures: " + solver.failures()); System.out.println(" branches: " + solver.branches()); System.out.println(" wall time: " + solver.wallTime() + "ms"); System.out.println(" Solutions found: " + solutionCount); } private NQueensCp() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.ConstraintSolver; public class NQueensCp { public static void Main(String[] args) { // Instantiate the solver. Solver solver = new Solver("N-Queens"); const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent()); // Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch(); // Statistics. Console.WriteLine("Statistics"); Console.WriteLine($" failures: {solver.Failures()}"); Console.WriteLine($" branches: {solver.Branches()}"); Console.WriteLine($" wall time: {solver.WallTime()} ms"); Console.WriteLine($" Solutions found: {SolutionCount}"); } }
솔루션 수
솔루션의 수는 보드의 크기에 따라 대략 기하급수적으로 증가합니다.
| 보드 크기 | 솔루션 | 모든 솔루션을 찾는 데 걸리는 시간 (밀리초) |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 2 | 0 |
| 5 | 10 | 0 |
| 6 | 4 | 0 |
| 7 | 40 | 3 |
| 8 | 92 | 9 |
| 9 | 352 | 35 |
| 10 | 724 | 95 |
| 11 | 2680 | 378 |
| 12 | 14200 | 2198 |
| 13 | 73712 | 11628 |
| 14 | 365596 | 62427 |
| 15 | 2279184 | 410701 |
대칭성이라는 기법으로 다른 해를 회전하는 것뿐인 해가 많습니다. 브레이킹 체인지를 사용하여 필요한 계산의 양을 줄일 수 있습니다. 우리는 여기서 위의 솔루션은 속도가 빠르지 않고 단순합니다. 물론 원하는 해결 방법을 찾는 대신 보드 크기가 최대 50인 경우 몇 밀리초가 채 걸리지 않습니다.
