ในส่วนต่อไปนี้ เราจะแสดงข้อจำกัดสำหรับการเขียนโปรแกรม (CP) โดย โจทย์แบบผสมผสานที่อิงจากเกมหมากรุก ในการเล่นหมากรุก ราชินีสามารถโจมตีได้ แนวนอน แนวตั้ง และแนวทแยงมุม ปัญหา N-queens ถามว่า
วิธีวางควีนไซส์บนกระดานหมากรุก NxN เพื่อไม่ให้มีสองคนโจมตี ระหว่างกัน
คุณสามารถดูวิธีแก้ปัญหาที่เป็นไปได้หนึ่งสำหรับโจทย์ N-queens สำหรับ N = 4
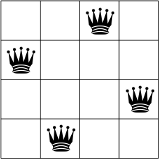
ไม่มีควีนสองตัวอยู่ในแถว คอลัมน์ หรือแนวทแยงมุมเดียวกัน
โปรดทราบว่านี่ไม่ใช่ปัญหาการเพิ่มประสิทธิภาพ เราต้องการหาทั้งหมดที่เป็นไปได้ โซลูชันที่เหมาะสมมากกว่า 1 โซลูชัน ซึ่งทำให้เป็นโซลูชันที่ลงตัว สำหรับการปรับโปรแกรมที่จำกัด ส่วนต่อไปนี้อธิบายวิธี CP สำหรับปัญหา N-queens และ นำเสนอโปรแกรมที่แก้โจทย์โดยใช้ทั้งตัวแก้โจทย์ CP-SAT และ CP ต้นฉบับ เครื่องมือแก้โจทย์ปัญหา
แนวทาง CP สำหรับโจทย์ N-queens
เครื่องมือแก้โจทย์ CP ทำงานอย่างเป็นระบบเพื่อพยายาม การกำหนดค่าที่เป็นไปได้ให้กับตัวแปรในโจทย์ เพื่อหาค่า โซลูชันที่เป็นไปได้ ในโจทย์ 4 ควีน เครื่องมือแก้โจทย์จะเริ่มที่ซ้ายสุด และวางควีนไซส์ 1 ตัวต่อเนื่องกันในแต่ละคอลัมน์ ในตำแหน่งที่ ที่ไม่ถูกโจมตีโดยราชินีแห่งใดก่อนหน้า
การเผยแพร่และการย้อนกลับ
มีองค์ประกอบสำคัญ 2 ประการที่ทำให้การค้นหาจำกัดการเขียนโปรแกรมมีดังนี้
- การเผยแพร่ — ทุกครั้งที่โปรแกรมแก้โจทย์กำหนดค่าให้กับตัวแปร ระบบจะ ข้อจำกัดเพิ่มข้อจำกัดสำหรับค่าที่เป็นไปได้ของ ตัวแปร ข้อจำกัดเหล่านี้จะมีผลไปยังการกำหนดตัวแปรในอนาคต เช่น ในโจทย์ 4 ควีน ทุกครั้งที่ตัวแก้โจทย์ใส่เลขควีน ไม่สามารถวางควีนตัวอื่นๆ บนแถวได้ และเส้นทแยงมุมที่ราชินีปัจจุบันเปิดอยู่ การเผยแพร่ สามารถเพิ่มความเร็วในการค้นหาได้อย่างมากโดยการลดชุดของ ค่าตัวแปรที่เครื่องมือแก้โจทย์ต้องสำรวจ
- การย้อนกลับเกิดขึ้นเมื่อเครื่องมือแก้โจทย์กำหนดค่าให้กับรายการถัดไปไม่ได้ เนื่องจากข้อจำกัด หรือหาทางแก้ ในทั้ง 2 กรณี ฟิลด์ ย้อนกลับไปยังขั้นตอนก่อนหน้าและเปลี่ยนค่าของตัวแปร ไปยังค่าที่ยังไม่เคยลองทำ ในตัวอย่างนี้ 4-queens ซึ่งหมายถึงการย้ายควีนไปยังสี่เหลี่ยมจัตุรัสใหม่ในคอลัมน์ปัจจุบัน
ถัดไป คุณจะดูวิธีที่โปรแกรมข้อจำกัดใช้การเผยแพร่และการย้อนกลับเพื่อ แก้โจทย์ 4-ควีน
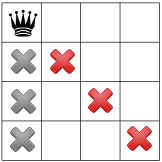
สมมติว่าเครื่องมือแก้โจทย์เริ่มด้วยการวางเลขควีนทางด้านซ้ายบนโดยไม่มีกฎเกณฑ์ ที่มุม นั่นก็เป็นสมมติฐานในหลายๆ เรื่อง และบางทีอาจทำให้ไม่มีวิธีแก้ปัญหา มีรูปราชินีอยู่ที่มุมซ้ายบน
จากสมมติฐานนี้ เราจะเผยแพร่ข้อจำกัดใดได้บ้าง ข้อจำกัดประการหนึ่งคือ สามารถมีควีนได้เพียง 1 รายในคอลัมน์ (เครื่องหมาย X สีเทาด้านล่าง) และอีกคอลัมน์หนึ่ง ข้อจำกัดห้ามควีนสองตัวบนเส้นทแยงมุมเดียวกัน (X สีแดงด้านล่าง)
ข้อจำกัดข้อที่ 3 ห้ามไม่ให้มีควีนอยู่ในแถวเดียวกัน
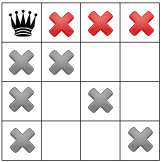
ข้อจำกัดของเราเผยแพร่ออกไป เราสามารถทดสอบสมมติฐานอื่น และวาง ควีนที่สองบนหนึ่งในกำลังสองที่เหลือ วิธีแก้ปัญหาของเราอาจตัดสินใจ เพื่อวางไว้ในสี่เหลี่ยมจัตุรัสแรกที่ใช้ได้ของคอลัมน์ที่สอง:
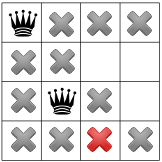
หลังจากเผยแพร่จุดยึดแนวทแยงแล้ว เราจะเห็นว่าเส้นยึดแนวทแยงไม่ สี่เหลี่ยมที่ใช้ได้ในคอลัมน์ที่ 3 หรือแถวสุดท้าย
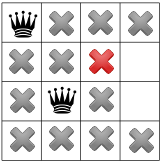
แม้จะยังไม่สามารถแก้ปัญหาได้ในช่วงนี้ เราจึงจำเป็นต้องถอยหลังไปก่อน ตัวเลือกหนึ่งคือ เพื่อให้เครื่องมือแก้โจทย์เลือกสี่เหลี่ยมจัตุรัสอีกค่าหนึ่งที่มีอยู่ในคอลัมน์ที่ 2 อย่างไรก็ตาม การจำกัดการเผยแพร่จะบังคับให้ควีนอยู่ในแถวที่สองของ คอลัมน์ที่ 3 โดยไม่ใส่ตำแหน่งสำหรับพระราชินีที่ 4 ไว้:

ดังนั้นตัวแก้โจทย์จึงต้องทำย้อนกลับอีกครั้ง คราวนี้กลับไปที่ฟังก์ชัน ตำแหน่งของสมเด็จพระราชินีนาถพระองค์แรก ตอนนี้เราได้แสดงให้เห็นว่าไม่มีวิธีแก้ปัญหาสำหรับราชินี จะอยู่ในมุมสี่เหลี่ยม
เนื่องจากจะไม่มีราชินีอยู่ตรงมุม เครื่องมือแก้โจทย์จึงย้ายราชินีพระองค์แรกลงมา ทีละ 1 และแพร่กระจายไป โดยเหลือไว้จุดเดียวสำหรับควีนที่ 2
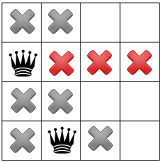
การเผยแพร่เนื้อหาอีกครั้งแสดงเพียงจุดเดียวที่เหลืออยู่สำหรับสมเด็จพระราชินีที่ 3
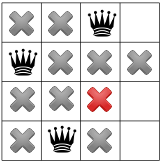
และสำหรับราชินีองค์ที่ 4 ซึ่งเป็นองค์สุดท้าย

เรามีโซลูชันแรก หากเราสั่งให้เครื่องมือแก้โจทย์หยุดหลังจากพบ โซลูชันแรกก็จะสิ้นสุดลงที่นี่ มิฉะนั้น จะเป็นการย้อนกลับมาอีก ให้วางควีนแรกในแถวที่สามของคอลัมน์แรก
โซลูชันที่ใช้ CP-SAT
ปัญหา N-queens เหมาะสมที่สุดสำหรับการเขียนโปรแกรมที่จำกัด ด้วยวิธีนี้ เราจะแนะนำโปรแกรม Python สั้นๆ ที่ใช้โปรแกรมแก้โจทย์ CP-SAT เพื่อ ค้นหาวิธีแก้ปัญหาทั้งหมด
นำเข้าไลบรารี
โค้ดต่อไปนี้จะนำเข้าไลบรารีที่จำเป็น
Python
import sys import time from ortools.sat.python import cp_model
C++
#include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h"
Java
import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr;
C#
using System; using Google.OrTools.Sat;
ประกาศโมเดล
โค้ดต่อไปนี้แจ้งโมเดล CP-SAT
Python
model = cp_model.CpModel()
C++
CpModelBuilder cp_model;
Java
CpModel model = new CpModel();
C#
CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
สร้างตัวแปร
เครื่องมือแก้โจทย์จะสร้างตัวแปรให้กับโจทย์เป็นอาร์เรย์ชื่อ queens
Python
# There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]
C++
// There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); }
Java
int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); }
C#
int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); }
ในที่นี้เราจะสมมติว่า queens[j] คือหมายเลขแถวของราชินีในคอลัมน์ j
กล่าวคือ queens[j] = i หมายความว่ามีราชินีอยู่ในแถว i และคอลัมน์ j
สร้างข้อจำกัด
นี่คือโค้ดที่สร้างข้อจำกัดสำหรับปัญหา
Python
# All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size))
C++
// The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2);
Java
// All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2);
C#
// All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2);
โค้ดจะใช้เมธอด AddAllDifferent ซึ่งต้องใช้องค์ประกอบทั้งหมดของ
ให้แตกต่างกันด้วย
มาดูกันว่าข้อจำกัดเหล่านี้รับประกันเงื่อนไข 3 ข้อสำหรับ N-queens ได้อย่างไร โจทย์ (ราชินีบนแถว คอลัมน์ และเส้นทแยงมุมต่างๆ)
ไม่มีควีนสองตัวในแถวเดียวกัน
การใช้เมธอด AllDifferent ของเครื่องมือแก้โจทย์กับ queens จะบังคับค่าของ
queens[j] ให้ต่างกันสำหรับ j แต่ละรายการ ซึ่งหมายความว่า ควีนไซส์ทั้งหมดต้องอยู่ใน
หลายแถว
ไม่มีควีนสองตัวในคอลัมน์เดียวกัน
ข้อจำกัดนี้โดยนัยในคำจำกัดความของ queens
เนื่องจากไม่มีองค์ประกอบ 2 อย่างของ queens ที่มีดัชนีเดียวกัน จึงไม่สามารถมี 2 ควีนได้
ในคอลัมน์เดียวกัน
ไม่มีควีนสองตัวบนแนวทแยงเดียวกัน
จุดยึดแนวทแยงจะยากกว่าจุดยึดแถวและคอลัมน์เล็กน้อย กรณีแรก หากพระราชินี 2 พระองค์อยู่บนเส้นทแยงมุมเดียวกัน จะมีเงื่อนไขอย่างใดอย่างหนึ่งต่อไปนี้ ต้องเป็นจริง
- หมายเลขแถวบวกหมายเลขคอลัมน์สำหรับราชินีทั้ง 2 ตัวเท่ากัน
กล่าวคือ
queens(j) + jมีค่าเท่ากันสำหรับดัชนี 2 รายการที่แตกต่างกันj - หมายเลขแถวลบหมายเลขคอลัมน์สำหรับราชินีทั้ง 2 ตัวเท่ากัน
ในกรณีนี้
queens(j) - jมีค่าเท่ากันสำหรับดัชนีj2 รายการที่แตกต่างกัน
หนึ่งในเงื่อนไขเหล่านี้หมายถึง พระราชินีทรงอยู่บนแนวทแยงมุมบนแนวทแยงที่เท่ากัน ( จากซ้ายไปขวา) ในขณะที่อีกช่องหนึ่งแปลว่าอยู่บนแนวเดียวกัน แบบทแยงมุม เงื่อนไขใดที่สอดคล้องกับน้อยไปมากและจากมากไปน้อย ขึ้นอยู่กับวิธีเรียงลำดับแถวและคอลัมน์ ตามที่กล่าวไว้ใน ส่วนก่อนหน้า การจัดลำดับจะไม่มีผลต่อชุดของ โซลูชันต่างๆ ขึ้นอยู่กับวิธีที่คุณนำเสนอภาพ
จุดยึดแนวทแยงคือค่าของ queens(j) + j ทั้งหมดต้องเป็น
และค่าของ queens(j) - j ต้องแตกต่างกันทั้งหมด
j ที่แตกต่างกัน
หากต้องการใช้เมธอด AddAllDifferent กับ queens(j) + j เราจะใส่อินสแตนซ์ N รายการ
ของตัวแปรสำหรับ j จาก 0 ถึง N-1 ลงในอาร์เรย์ diag1 ดังนี้
q1 = model.NewIntVar(0, 2 * board_size, 'diag1_%i' % i) diag1.append(q1) model.Add(q1 == queens[j] + j)
จากนั้นเราจะใช้ AddAllDifferent กับ diag1
model.AddAllDifferent(diag1)
ข้อจำกัดสำหรับ queens(j) - j สร้างขึ้นในทำนองเดียวกัน
สร้างเครื่องพิมพ์โซลูชัน
ในการพิมพ์วิธีแก้ปัญหา N-queens ทั้งหมด คุณจะต้องผ่าน Callback ที่เรียกว่าเครื่องพิมพ์โซลูชันไปยังเครื่องมือแก้โจทย์ CP-SAT Callback จะพิมพ์แต่ละรายการ ใหม่ที่เครื่องมือแก้โจทย์พบเจอ โค้ดต่อไปนี้สร้างโซลูชัน เครื่องพิมพ์
Python
class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print()
C++
int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; }));
Java
static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; }
C#
public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; }
โปรดทราบว่าเครื่องพิมพ์โซลูชันจะต้องเขียนเป็นคลาส Python เนื่องจาก อินเทอร์เฟซ Python ไปยังโปรแกรมแก้โจทย์ C++ ที่สำคัญ
โซลูชันจะพิมพ์ด้วยบรรทัดต่อไปนี้ในเครื่องพิมพ์โซลูชัน
for v in self.__variables: print('%s = %i' % (v, self.Value(v)), end = ' ')
ในตัวอย่างนี้ self.__variables คือตัวแปร queens และแต่ละ v
ตรงกับหนึ่งในแปดรายการของ queens วิธีนี้จะพิมพ์โซลูชันใน
แบบฟอร์มต่อไปนี้: x0 = queens(0) x1 = queens(1) ... x7 = queens(7) โดยที่
xi คือหมายเลขคอลัมน์ของราชินีในแถว i
ส่วนถัดไปจะแสดงตัวอย่างโซลูชัน
เรียกใช้เครื่องมือแก้โจทย์และแสดงผลลัพธ์
โค้ดต่อไปนี้จะเรียกใช้เครื่องมือแก้โจทย์และแสดงโซลูชัน
Python
solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer)
C++
// Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions;
Java
CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb);
C#
// Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb);
โปรแกรมค้นหาโซลูชันที่แตกต่างกัน 92 รายการสำหรับกระดานขนาด 8x8 นี่คือคำถามข้อแรก
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Solutions found: 92คุณสามารถแก้โจทย์สำหรับกระดานขนาดอื่นได้โดยส่งคำ N เป็น
อาร์กิวเมนต์บรรทัดคำสั่ง ตัวอย่างเช่น หากโปรแกรมชื่อ queens
python nqueens_sat.py 6 ช่วยแก้ปัญหาสำหรับกระดานขนาด 6x6
ทั้งโปรแกรม
นี่คือข้อมูลทั้งหมดของโปรแกรม N-queens
Python
"""OR-Tools solution to the N-queens problem.""" import sys import time from ortools.sat.python import cp_model class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() def main(board_size: int) -> None: # Creates the solver. model = cp_model.CpModel() # Creates the variables. # There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size)) # Solve the model. solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer) # Statistics. print("\nStatistics") print(f" conflicts : {solver.num_conflicts}") print(f" branches : {solver.num_branches}") print(f" wall time : {solver.wall_time} s") print(f" solutions found: {solution_printer.solution_count}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h" namespace operations_research { namespace sat { void NQueensSat(const int board_size) { // Instantiate the solver. CpModelBuilder cp_model; // There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2); int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; })); // Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions; // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << CpSolverResponseStats(response); } } // namespace sat } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { if (!absl::SimpleAtoi(argv[1], &board_size)) { LOG(INFO) << "Cannot parse '" << argv[1] << "', using the default value of 8."; board_size = 8; } } operations_research::sat::NQueensSat(board_size); return EXIT_SUCCESS; }
Java
package com.google.ortools.sat.samples; import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr; /** OR-Tools solution to the N-queens problem. */ public final class NQueensSat { static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; } public static void main(String[] args) { Loader.loadNativeLibraries(); // Create the model. CpModel model = new CpModel(); int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2); // Create a solver and solve the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb); // Statistics. System.out.println("Statistics"); System.out.println(" conflicts : " + solver.numConflicts()); System.out.println(" branches : " + solver.numBranches()); System.out.println(" wall time : " + solver.wallTime() + " s"); System.out.println(" solutions : " + cb.getSolutionCount()); } private NQueensSat() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.Sat; public class NQueensSat { public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; } static void Main() { // Constraint programming engine CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
โซลูชันที่ใช้ตัวแก้โจทย์ CP ดั้งเดิม
ส่วนต่อไปนี้นำเสนอโปรแกรม Python ที่แก้โจทย์ N-queens โดยใช้ เครื่องมือแก้โจทย์ CP แบบดั้งเดิม (อย่างไรก็ตาม เราขอแนะนำให้ใช้เครื่องมือแก้โจทย์ CP-SAT เวอร์ชันใหม่)
นำเข้าไลบรารี
โค้ดต่อไปนี้จะนำเข้าไลบรารีที่จำเป็น
Python
import sys from ortools.constraint_solver import pywrapcp
C++
#include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h"
Java
import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver;
C#
using System; using Google.OrTools.ConstraintSolver;
ประกาศเครื่องมือแก้โจทย์
โค้ดต่อไปนี้เป็นการประกาศเครื่องมือแก้โจทย์ CP ดั้งเดิม
Python
solver = pywrapcp.Solver("n-queens")
C++
Solver solver("N-Queens");
Java
Solver solver = new Solver("N-Queens");
C#
Solver solver = new Solver("N-Queens");
สร้างตัวแปร
เมธอด IntVar ของเครื่องมือแก้โจทย์จะสร้างตัวแปรของโจทย์เป็นอาร์เรย์
ชื่อ queens
Python
# The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]
C++
std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); }
Java
int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); }
C#
const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); }
สําหรับวิธีแก้โจทย์ใดก็ตาม queens[j] = i หมายถึงมีราชินีในคอลัมน์ j และแถว
i
สร้างข้อจำกัด
นี่คือโค้ดที่สร้างข้อจำกัดสำหรับปัญหา
Python
# All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))
C++
// The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2));
Java
// All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2));
C#
// All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent());
ข้อจำกัดเหล่านี้รับประกันเงื่อนไข 3 ข้อสำหรับปัญหา N-queens ( ควีนตามแถว คอลัมน์ และเส้นทแยงมุมต่างๆ)
ไม่มีควีนสองตัวในแถวเดียวกัน
การใช้เมธอด AllDifferent ของเครื่องมือแก้โจทย์กับ queens จะบังคับค่าของ
queens[j] ให้ต่างกันสำหรับ j แต่ละรายการ ซึ่งหมายความว่า ควีนไซส์ทั้งหมดต้องอยู่ใน
หลายแถว
ไม่มีควีนสองตัวในคอลัมน์เดียวกัน
ข้อจำกัดนี้โดยนัยในคำจำกัดความของ queens
เนื่องจากไม่มีองค์ประกอบ 2 อย่างของ queens ที่มีดัชนีเดียวกัน จึงไม่สามารถมี 2 ควีนได้
ในคอลัมน์เดียวกัน
ไม่มีควีนสองตัวบนแนวทแยงเดียวกัน
จุดยึดแนวทแยงจะยากกว่าจุดยึดแถวและคอลัมน์เล็กน้อย ประการแรก หากพระราชินี 2 พระองค์อยู่บนเส้นทแยงมุมเดียวกัน ข้อใดเป็นความจริงดังต่อไปนี้
- ถ้าเส้นทแยงมุมต่ำลงมา (จากซ้ายไปขวา) เลขแถวบวก
หมายเลขคอลัมน์สำหรับพระราชินีทั้งสองมีค่าเท่ากัน ดังนั้น
queens(i) + iมีเมธอด ค่าเดียวกันสำหรับ 2 ดัชนีที่แตกต่างกันi - ถ้าเส้นทแยงมุมต่ำลงมา เลขที่แถวลบด้วยหมายเลขคอลัมน์ของแต่ละส่วน
ของพระราชินี 2 พระองค์เท่าๆ กัน ในกรณีนี้
queens(i) - iมีค่าเท่ากัน สำหรับดัชนี 2 รายการที่มีi
จุดยึดแนวทแยงคือค่าของ queens(i) + i ทั้งหมดต้องเป็น
และในทำนองเดียวกัน ค่าของ queens(i) - i ก็ต้องแตกต่างกันด้วย
i ที่แตกต่างกัน
โค้ดด้านบนจะเพิ่มข้อจำกัดนี้โดยใช้
AllDifferent
เป็น queens[j] + j และ queens[j] - j สำหรับ i แต่ละเมธอด
เพิ่มเครื่องมือสร้างการตัดสินใจ
ขั้นตอนถัดไปคือการสร้างเครื่องมือสร้างการตัดสินใจ ซึ่งจะกำหนดกลยุทธ์การค้นหา สำหรับโจทย์แล้ว กลยุทธ์การค้นหา อาจส่งผลอย่างมากต่อเวลาการค้นหา เนื่องจากการเผยแพร่ข้อจำกัด ซึ่งลดจำนวนค่าตัวแปร เครื่องมือแก้โจทย์ต้องสำรวจ คุณได้เห็นตัวอย่างแล้วใน ตัวอย่าง 4-queens
โค้ดต่อไปนี้จะสร้างตัวสร้างการตัดสินใจโดยใช้เครื่องมือแก้โจทย์
Phase
Python
db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
C++
DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);
Java
// Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
C#
// Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
โปรดดูเครื่องมือสร้างการตัดสินใจสำหรับรายละเอียดเกี่ยวกับ
ในเมธอด Phase
วิธีการทำงานของเครื่องมือสร้างการตัดสินใจในตัวอย่าง 4-queens
มาดูกันว่าเครื่องมือสร้างการตัดสินใจกำหนดทิศทางการค้นหาใน
ตัวอย่าง 4-queens
เครื่องมือแก้โจทย์ควรเริ่มต้นด้วย queens[0] ซึ่งเป็นตัวแปรแรกในอาร์เรย์ตามที่แนะนำ
โดย CHOOSE_FIRST_UNBOUND เครื่องมือแก้โจทย์จะกำหนด queens[0] ให้น้อยที่สุด
ค่าที่ยังไม่ได้ลองใช้ ซึ่งเท่ากับ 0 ในขั้นนี้ ตามที่ระบุโดย
ASSIGN_MIN_VALUE โดยวางควีนแห่งแรกไว้ที่มุมซ้ายบนของ
ถัดไป เครื่องมือแก้โจทย์เลือก queens[1] ซึ่งเป็นตัวแปรแรกที่ไม่มีขอบเขตใน
queens หลังจากเผยแพร่ข้อจำกัดแล้ว อาจมีแถวที่เป็นไปได้ 2 แถวสำหรับ
ควีนในคอลัมน์ 1: แถว 2 หรือแถว 3 ตัวเลือก ASSIGN_MIN_VALUE จะกำหนดเส้นทาง
ให้กำหนด queens[1] = 2 (แต่หากคุณตั้งค่า IntValueStrategy เป็น
ASSIGN_MAX_VALUE เครื่องมือแก้โจทย์จะกำหนด queens[1] = 3)
คุณตรวจสอบได้ว่าการค้นหาที่เหลือเป็นไปตามกฎเดียวกันหรือไม่
เรียกใช้เครื่องมือแก้โจทย์และแสดงผลลัพธ์
โค้ดต่อไปนี้จะเรียกใช้เครื่องมือแก้โจทย์และแสดงโซลูชัน
Python
# Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch()
C++
// Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch();
Java
int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch();
C#
// Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch();
นี่คือโซลูชันแรกที่โปรแกรมพบสำหรับกระดานขนาด 8x8
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Statistics
failures: 304
branches: 790
wall time: 5 ms
Solutions found: 92คุณสามารถแก้โจทย์สำหรับกระดานขนาดอื่นได้โดยส่งคำ N เป็น
อาร์กิวเมนต์บรรทัดคำสั่ง เช่น python nqueens_cp.py 6 จะแก้โจทย์
สำหรับกระดานขนาด 6x6
ทั้งโปรแกรม
โปรแกรมที่สมบูรณ์แสดงอยู่ด้านล่าง
Python
"""OR-Tools solution to the N-queens problem.""" import sys from ortools.constraint_solver import pywrapcp def main(board_size): # Creates the solver. solver = pywrapcp.Solver("n-queens") # Creates the variables. # The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)])) db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE) # Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch() # Statistics. print("\nStatistics") print(f" failures: {solver.Failures()}") print(f" branches: {solver.Branches()}") print(f" wall time: {solver.WallTime()} ms") print(f" Solutions found: {num_solutions}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h" namespace operations_research { void NQueensCp(const int board_size) { // Instantiate the solver. Solver solver("N-Queens"); std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2)); DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch(); // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << " failures: " << solver.failures(); LOG(INFO) << " branches: " << solver.branches(); LOG(INFO) << " wall time: " << solver.wall_time() << " ms"; LOG(INFO) << " Solutions found: " << num_solutions; } } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { board_size = std::atoi(argv[1]); } operations_research::NQueensCp(board_size); return EXIT_SUCCESS; }
Java
// OR-Tools solution to the N-queens problem. package com.google.ortools.constraintsolver.samples; import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver; /** N-Queens Problem. */ public final class NQueensCp { public static void main(String[] args) { Loader.loadNativeLibraries(); // Instantiate the solver. Solver solver = new Solver("N-Queens"); int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2)); // Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch(); // Statistics. System.out.println("Statistics"); System.out.println(" failures: " + solver.failures()); System.out.println(" branches: " + solver.branches()); System.out.println(" wall time: " + solver.wallTime() + "ms"); System.out.println(" Solutions found: " + solutionCount); } private NQueensCp() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.ConstraintSolver; public class NQueensCp { public static void Main(String[] args) { // Instantiate the solver. Solver solver = new Solver("N-Queens"); const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent()); // Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch(); // Statistics. Console.WriteLine("Statistics"); Console.WriteLine($" failures: {solver.Failures()}"); Console.WriteLine($" branches: {solver.Branches()}"); Console.WriteLine($" wall time: {solver.WallTime()} ms"); Console.WriteLine($" Solutions found: {SolutionCount}"); } }
จำนวนโซลูชัน
จำนวนโซลูชันจะเพิ่มขึ้นประมาณเท่าตัวตามขนาดของกระดาน ดังนี้
| ขนาดกระดาน | โซลูชัน | เวลาที่ใช้ในการค้นหาโซลูชันทั้งหมด (มิลลิวินาที) |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 2 | 0 |
| 5 | 10 | 0 |
| 6 | 4 | 0 |
| 7 | 40 | 3 |
| 8 | 92 | 9 |
| 9 | 352 | 35 |
| 10 | 724 | 95 |
| 11 | 2680 | 378 |
| 12 | 14200 | 2198 |
| 13 | 73712 | 11628 |
| 14 | 365596 | 62427 |
| 15 | 2279184 | 410701 |
สารละลายจำนวนมากเป็นเพียงการหมุนของคนอื่น และเทคนิคที่เรียกว่าสมมาตร ช่วงพักโฆษณาสามารถใช้เพื่อลดจำนวนการคำนวณที่ต้องการ เราไม่ได้ใช้ ที่ระบุไว้ที่นี่ โซลูชันข้างต้นของเราไม่ได้มุ่งหวังให้เป็นไปอย่างรวดเร็ว ง่ายเท่านั้น แน่นอน เราจะทำให้ทุกอย่างเร็วขึ้นได้ ถ้าต้องการค้นหาโซลูชันเพียงอย่างเดียว แทนที่จะ ทั้งหมด หมายถึงไม่เกิน 2-3 มิลลิวินาทีสำหรับกระดานขนาดไม่เกิน 50 อักขระ
