İlerleyen bölümlerde, kısıt programlamanın (CP) en az bir satranç oyununa dayalı bir kombinasyon problemi. Satrançta kraliçe saldırabilir şekilde düzenleyebilirsiniz. N-queens problemi şu soruları soruyor:
NxN satranç tahtasına yerleştirilerek iki tanesinin saldırıya uğramaması birbirimizle nasıl?
Aşağıda, N = 4 için N-queens probleminin olası bir çözümünü görebilirsiniz.
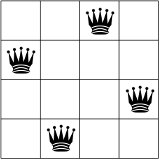
Aynı sıra, sütun veya köşegen üzerinde iki ana ergen simgesi yoktur.
Bunun bir optimizasyon sorunu olmadığını unutmayın: olası tüm olası çözümleri tercih eder. Bu da onu doğal bir aday haline getirir. bir örneğidir. Aşağıdaki bölümlerde N-queens problemi için CP yaklaşımı açıklanmaktadır ve hem CP-SAT çözücüyü hem de orijinal CP'yi kullanarak problemi çözen programlar sunma çözücü olarak kullanılır.
N-queens problemine CP yaklaşımı
CP çözücü, tüm çözümleri sistematik olarak bir problemdeki değişkenlere olası değer atamalarını mantıklı çözümler üzerinde çalışıyoruz. Dörtlü soruda çözücü en soldakinden başlar sütununa ve arka arkaya her sütuna tarafından saldırıya uğramadığı konusunda iyi bir örnektir.
Yayma ve geri izleme
Kısıtlama programlama aramasının iki temel öğesi vardır:
- Çoğaltma: Çözücü bir değişkene her değer atadığında, kısıtlamalar, atanmamış öğelerin olası değerlerine kısıtlamalar ekler değişkenlerine karşılık gelir. Bu kısıtlamalar gelecekteki değişken atamalarına yayılır. Örneğin, 4-kraliçe probleminde, çözücü bir kraliçeyi her yerleştirdiğinde, sıraya başka bir kraliçe yerleştirilemez. Yayma, veri kümesi sayısını azaltarak aramayı önemli ölçüde çözücünün keşfetmesi gereken değişken değerleridir.
- Geri izleme, çözücüden biri bir sonraki değişkeninin kısıtlanmasını engeller veya bir çözüm bulur. Her iki durumda da, çözücü, önceki bir aşamaya geri döner ve değişkenin değerini daha önce denenmemiş bir değere dönüştürün. Dört kişilik örneğinde, Bu, bir kraliçenin mevcut sütunda yeni bir kareye taşınması anlamına gelir.
Bunun ardından, kısıt programlamanın problemi çözmek için sabırsızlanıyorum.
Çözücünün rastgele bir şekilde sol üste bir vezir yerleştirerek başladığını varsayalım köşesindeki kartı tıklayın. Bu bir tür hipotez. belki de ortaya çıkabilecek bir sorunun sol üst köşesinde bir analog var.
Bu hipotezi göz önünde bulundurarak, hangi kısıtlamaları yayabiliriz? Bir kısıtlama, bir sütunda yalnızca bir tane veli (aşağıdaki gri X'ler) ve başka bir tane daha olabilir kısıtlama, aynı köşegen üzerinde iki veliye (aşağıdaki kırmızı X'ler) izin vermez.
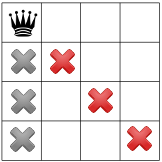
Üçüncü kısıtlamamız, velilerin aynı satırda olmasını yasaklar:
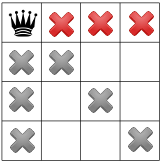
Kısıtlamalarımız yayıldı, başka bir hipotezi test edebilir ve kalan karelerden birinde ikinci velisi olacak. Çözme aracımız bunu, ikinci sütundaki ilk uygun kareyi yerleştirir:
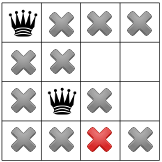
Köşegen kısıtlamasını yayımladıktan sonra, köşegen kısıtın son satırdaki kullanılabilir kareleri bulun:
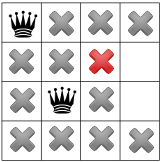
Bu aşamada hiçbir çözüm mümkün olmadığı için geriye dönmemiz gerekiyor. Seçeneklerden biri ikinci sütunda mevcut diğer kareyi seçmesini sağlar. Ancak, kısıtlama yayılımı, bir veziri grafiğin ikinci satırına zorlar. üçüncü sütunda dördüncü vezek için geçerli hiçbir yer kalmaz:

Çözücünün tekrar geri gitmesi gerekir. Bu seferki karartın. Artık kraliçelere bir çözümün olmadığını gösterdik. köşedeki kareyi işgal eder.
Köşede veli olamayacağı için çözücü ilk veziciyi aşağı hareket ettirir bir ile birleşir ve yayılır, ikincisi için yalnızca bir nokta bırakır.
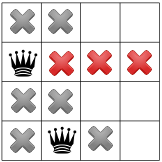
Çoğaltma tekrar yapıldığında üçüncü vezek için yalnızca tek bir yer belirir:
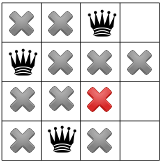
Dördüncü ve son kraliçe için:

İlk çözümümüzü sunduk! Problem çözme aracımıza burada biter. Aksi takdirde, proje bu süreçte ilk veliyi, ilk sütunun üçüncü satırına yerleştirin.
CP-SAT kullanan çözüm
N-queens problemi ideal olarak kısıt programlamaya uygundur. Burada bölümünde CP-SAT çözücüyü kullanan kısa bir Python programını bir çözüm bulmanız gerekir.
Kitaplıkları içe aktarma
Aşağıdaki kod, gerekli kitaplığı içe aktarır.
Python
import sys import time from ortools.sat.python import cp_model
C++
#include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h"
Java
import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr;
C#
using System; using Google.OrTools.Sat;
Modeli açıklama
Aşağıdaki kod CP-SAT modelini tanımlar.
Python
model = cp_model.CpModel()
C++
CpModelBuilder cp_model;
Java
CpModel model = new CpModel();
C#
CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
Değişkenleri oluşturma
Çözücü, problem için değişkenleri queens adında bir dizi olarak oluşturur.
Python
# There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]
C++
// There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); }
Java
int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); }
C#
int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); }
Burada, queens[j] sütununun j sütunundaki velinin satır numarası olduğunu varsayıyoruz.
Diğer bir deyişle queens[j] = i, i. satır ve j. sütunda bir vezir olduğu anlamına gelir.
Kısıtlamaları oluşturma
Sorunla ilgili kısıtlamaları oluşturan kodu burada görebilirsiniz.
Python
# All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size))
C++
// The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2);
Java
// All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2);
C#
// All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2);
Kod, AddAllDifferent yöntemini kullanır. Bu yöntem, bir
değişken dizisi farklı olacaktır.
Bu kısıtlamaların N-queens için üç koşulu nasıl garanti ettiğini görelim problemi (farklı satırlar, sütunlar ve köşegenlerdeki kraliçeler) içerir.
Aynı sırada iki vezon yok
Çözücünün AllDifferent yöntemini queens hücresine uygulamak, şunun değerlerini zorlar:
queens[j] her j için farklı olmalıdır, yani tüm vezirler ekipte olmalıdır
görebilirsiniz.
Aynı sütunda iki kraliçe yoktur
Bu kısıtlama, queens tanımında örtülüdür.
queens öğesinin hiçbir öğesi aynı dizine sahip olamayacağından iki kraliçe olamaz
değerini girin.
Aynı köşegen üzerinde iki vezan yoktur
Çapraz kısıt, satır ve sütun kısıtlamalarına göre biraz daha karmaşıktır. Birincisi, iki vezir aynı köşegen üzerinde yer alıyorsa aşağıdaki koşullardan biri doğru olmalıdır:
- İki kraliçenin her biri için satır numarası ile sütun numarası eşittir.
Yani
queens(j) + j, iki farklı dizin için aynı değere sahipj. - Satır numarası eksi sütun numarası her iki veli için eşittir.
Bu durumda
queens(j) - j, iki farklı dizin (j) için aynı değere sahiptir.
Bu koşullardan biri, vezirlerin aynı artan köşegen üzerinde ( soldan sağa doğru), diğeri ise aynı inişli çıkışta yer alır. olmalıdır. Hangi koşul artan, hangisi azalana karşılık gelir , satır ve sütunları nasıl sıraladığınıza bağlıdır. Şurada belirtildiği gibi: bölümünü seçerseniz, sıralamanın görselleştirdiğinize bağlı olarak değişiyor.
Köşegen kısıtlaması şu şekildedir: queens(j) + j değerlerinin tümünün
farklı ve queens(j) - j değerlerinin tümü farklı olmalıdır;
farklı j.
AddAllDifferent yöntemini queens(j) + j öğesine uygulamak için N örneğini koyduk
değeri, 0 ile N-1 arasında, j için aşağıdaki gibi bir diziye (diag1) dönüştürülsün:
q1 = model.NewIntVar(0, 2 * board_size, 'diag1_%i' % i) diag1.append(q1) model.Add(q1 == queens[j] + j)
Ardından diag1 öğesine AddAllDifferent uygularız.
model.AddAllDifferent(diag1)
queens(j) - j kısıtlaması benzer şekilde oluşturulur.
Çözüm yazıcısı oluşturun
N-queens probleminin tüm çözümlerini yazdırmak için bir geri arama iletmeniz gerekir. çözüm yazıcısı olarak adlandırılır. Geri çağırma, çözücü bulduğunda yeni bir çözüm bulur. Aşağıdaki kod bir çözüm oluşturur sağlayabilir.
Python
class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print()
C++
int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; }));
Java
static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; }
C#
public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; }
Çözüm yazıcısının Python sınıfı olarak yazılması gerektiğini unutmayın. Temel C++ çözücü için Python arayüzü.
Çözümler, çözüm yazıcısında aşağıdaki satırlarla yazdırılır.
for v in self.__variables: print('%s = %i' % (v, self.Value(v)), end = ' ')
Bu örnekte self.__variables, queens değişkeni ve her bir v değişkeni
queens öğesinin sekiz girişinden birine karşılık gelir. Bu şekilde bir çözüm yazdırılır
şu formu kullanın: x0 = queens(0) x1 = queens(1) ... x7 = queens(7) burada
xi, i. satırdaki veznenin sütun numarası.
Sonraki bölümde bir çözüm örneği gösterilmektedir.
Çözücüyü çağırın ve sonuçları görüntüleyin
Aşağıdaki kod çözücüyü çalıştırır ve çözümleri gösterir.
Python
solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer)
C++
// Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions;
Java
CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb);
C#
// Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb);
Program, 8x8 boyutlu bir pano için 92 farklı çözüm buluyor. İşte ilki.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Solutions found: 92Farklı büyüklükteki bir panonun problemini çözmek için N’yi
komut satırı bağımsız değişkeni anlamına gelir. Örneğin, programın adı queens ise
python nqueens_sat.py 6, 6x6 pano sorununu çözer.
Programın tamamı
N-queens programıyla ilgili programın tamamı burada.
Python
"""OR-Tools solution to the N-queens problem.""" import sys import time from ortools.sat.python import cp_model class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() def main(board_size: int) -> None: # Creates the solver. model = cp_model.CpModel() # Creates the variables. # There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size)) # Solve the model. solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer) # Statistics. print("\nStatistics") print(f" conflicts : {solver.num_conflicts}") print(f" branches : {solver.num_branches}") print(f" wall time : {solver.wall_time} s") print(f" solutions found: {solution_printer.solution_count}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h" namespace operations_research { namespace sat { void NQueensSat(const int board_size) { // Instantiate the solver. CpModelBuilder cp_model; // There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2); int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; })); // Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions; // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << CpSolverResponseStats(response); } } // namespace sat } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { if (!absl::SimpleAtoi(argv[1], &board_size)) { LOG(INFO) << "Cannot parse '" << argv[1] << "', using the default value of 8."; board_size = 8; } } operations_research::sat::NQueensSat(board_size); return EXIT_SUCCESS; }
Java
package com.google.ortools.sat.samples; import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr; /** OR-Tools solution to the N-queens problem. */ public final class NQueensSat { static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; } public static void main(String[] args) { Loader.loadNativeLibraries(); // Create the model. CpModel model = new CpModel(); int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2); // Create a solver and solve the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb); // Statistics. System.out.println("Statistics"); System.out.println(" conflicts : " + solver.numConflicts()); System.out.println(" branches : " + solver.numBranches()); System.out.println(" wall time : " + solver.wallTime() + " s"); System.out.println(" solutions : " + cb.getSolutionCount()); } private NQueensSat() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.Sat; public class NQueensSat { public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; } static void Main() { // Constraint programming engine CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
Orijinal CP çözücüyü kullanarak çözüm
Aşağıdaki bölümlerde, N-queens problemlerini çözmek için orijinal CP çözücü (Bununla birlikte, daha yeni CP-SAT çözücüyü kullanmanızı öneririz)
Kitaplıkları içe aktarma
Aşağıdaki kod, gerekli kitaplığı içe aktarır.
Python
import sys from ortools.constraint_solver import pywrapcp
C++
#include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h"
Java
import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver;
C#
using System; using Google.OrTools.ConstraintSolver;
Çözücüyü açıklama
Aşağıdaki kod, orijinal CP çözücüyü tanımlar.
Python
solver = pywrapcp.Solver("n-queens")
C++
Solver solver("N-Queens");
Java
Solver solver = new Solver("N-Queens");
C#
Solver solver = new Solver("N-Queens");
Değişkenleri oluşturma
Çözücünün IntVar yöntemi, probleme ilişkin değişkenleri dizi olarak oluşturur
queens adlı.
Python
# The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]
C++
std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); }
Java
int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); }
C#
const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); }
Herhangi bir çözüm için queens[j] = i, j sütununda ve satırda bir vezir olduğu anlamına gelir
i.
Kısıtlamaları oluşturma
Sorunla ilgili kısıtlamaları oluşturan kodu burada görebilirsiniz.
Python
# All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))
C++
// The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2));
Java
// All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2));
C#
// All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent());
Bu kısıtlamalar, N-queens problemi için üç koşulu garanti eder ( şeklinde iki ayrı satır, sütun ve köşegenlerdeki resimleri gösterir).
Aynı sırada iki vezon yok
Çözücünün AllDifferent yöntemini queens hücresine uygulamak, şunun değerlerini zorlar:
queens[j] her j için farklı olmalıdır, yani tüm vezirler ekipte olmalıdır
görebilirsiniz.
Aynı sütunda iki kraliçe yoktur
Bu kısıtlama, queens tanımında örtülüdür.
queens öğesinin hiçbir öğesi aynı dizine sahip olamayacağından iki kraliçe olamaz
değerini girin.
Aynı köşegen üzerinde iki vezan yoktur
Çapraz kısıt, satır ve sütun kısıtlamalarına göre biraz daha karmaşıktır. İlk olarak, iki vezir aynı köşegen üzerinde yer alıyorsa aşağıdakilerden biri doğru olmalıdır:
- Köşegen alçalan ise (soldan sağa doğru), satır numarası artı
sütun numarasının eşit olduğunu unutmayın. Yani
queens(i) + i, iki farklı dizin (i) için aynı değere sahiptir. - Köşegen artan düzende satır numarası eksi her bir öğe için sütun numarası
eşit. Bu durumda,
queens(i) - iaynı değere sahip olur iki farklı dizin (i) için gösterilir.
Köşegen kısıtlaması şu şekildedir: queens(i) + i değerlerinin tümünün
aynı şekilde queens(i) - i değerlerinin tamamı da farklı olmalıdır,
farklı i.
Yukarıdaki kod,
AllDifferent
yöntemini queens[j] + j ve queens[j] - j olarak ayarlayın (her i için).
Karar oluşturucuyu ekleme
Bir sonraki adım, Arama Ağı stratejisini ayarlayan bir karar oluşturucu oluşturmaktır. bir cümle ekleyebilirsiniz. Arama stratejisinin arama süresinde, kısıtlamaların yayılması nedeniyle, değişken değerlerin sayısını azaltır keşfetmesi gerekir. Bunun bir örneğini 4-kraliçe örneği.
Aşağıdaki kod, problem çözme aracının
Phase
yöntemidir.
Python
db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
C++
DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);
Java
// Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
C#
// Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
Ayrıntılı bilgi için Karar oluşturucu'ya
Phase yöntemine giriş bağımsız değişkenleri.
4-kraliçe örneğinde karar oluşturucunun işleyiş şekli
Şimdi, Karar Oluşturucu'nun Arama Ağı'nda aramayı nasıl yönlendirdiğine
4-kraliçe örneği.
Çözücü, dizideki ilk değişken olan queens[0] ile başlar.
CHOOSE_FIRST_UNBOUND tarafından. Çözücü daha sonra queens[0] için en küçük
(bu aşamada 0'dır), yani
ASSIGN_MIN_VALUE. Bunu yaptığınızda ilk veli, sayfanın sol üst köşesine
panosu.
Ardından çözücü, queens[1] seçimini yapar. Bu,
queens. Kısıtlamaları yayımladıktan sonra, bir
satır 1: satır 2 veya satır 3'ü seçin. ASSIGN_MIN_VALUE seçeneği
atanacak çözücü queens[1] = 2. (Bunun yerine IntValueStrategy öğesini
ASSIGN_MAX_VALUE, çözücü queens[1] = 3 değerini atar.)
Aramanın geri kalanının aynı kurallara uyup uymadığını kontrol edebilirsiniz.
Çözücüyü çağırın ve sonuçları görüntüleyin
Aşağıdaki kod çözücüyü çalıştırır ve çözümü gösterir.
Python
# Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch()
C++
// Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch();
Java
int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch();
C#
// Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch();
İşte programın 8x8 boyutlu pano için bulduğu ilk çözüm.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Statistics
failures: 304
branches: 790
wall time: 5 ms
Solutions found: 92Farklı büyüklükteki bir panonun problemini çözmek için N’yi
komut satırı bağımsız değişkeni anlamına gelir. Örneğin, python nqueens_cp.py 6 sorunu çözer
bir grafik bulunuyor.
Programın tamamı
Programın tamamı aşağıda gösterilmektedir.
Python
"""OR-Tools solution to the N-queens problem.""" import sys from ortools.constraint_solver import pywrapcp def main(board_size): # Creates the solver. solver = pywrapcp.Solver("n-queens") # Creates the variables. # The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)])) db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE) # Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch() # Statistics. print("\nStatistics") print(f" failures: {solver.Failures()}") print(f" branches: {solver.Branches()}") print(f" wall time: {solver.WallTime()} ms") print(f" Solutions found: {num_solutions}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h" namespace operations_research { void NQueensCp(const int board_size) { // Instantiate the solver. Solver solver("N-Queens"); std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2)); DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch(); // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << " failures: " << solver.failures(); LOG(INFO) << " branches: " << solver.branches(); LOG(INFO) << " wall time: " << solver.wall_time() << " ms"; LOG(INFO) << " Solutions found: " << num_solutions; } } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { board_size = std::atoi(argv[1]); } operations_research::NQueensCp(board_size); return EXIT_SUCCESS; }
Java
// OR-Tools solution to the N-queens problem. package com.google.ortools.constraintsolver.samples; import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver; /** N-Queens Problem. */ public final class NQueensCp { public static void main(String[] args) { Loader.loadNativeLibraries(); // Instantiate the solver. Solver solver = new Solver("N-Queens"); int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2)); // Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch(); // Statistics. System.out.println("Statistics"); System.out.println(" failures: " + solver.failures()); System.out.println(" branches: " + solver.branches()); System.out.println(" wall time: " + solver.wallTime() + "ms"); System.out.println(" Solutions found: " + solutionCount); } private NQueensCp() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.ConstraintSolver; public class NQueensCp { public static void Main(String[] args) { // Instantiate the solver. Solver solver = new Solver("N-Queens"); const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent()); // Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch(); // Statistics. Console.WriteLine("Statistics"); Console.WriteLine($" failures: {solver.Failures()}"); Console.WriteLine($" branches: {solver.Branches()}"); Console.WriteLine($" wall time: {solver.WallTime()} ms"); Console.WriteLine($" Solutions found: {SolutionCount}"); } }
Çözümlerin sayısı
Çözümlerin sayısı, panonun boyutuna göre kabaca katlanarak artar:
| Pano boyutu | Çözümler | Tüm çözümleri bulma süresi (ms) |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 2 | 0 |
| 5 | 10 | 0 |
| 6 | 4 | 0 |
| 7 | 40 | 3 |
| 8 | 92 | 9 |
| 9 | 352 | 35 |
| 10 | 724 | 95 |
| 11 | 2680 | 378 |
| 12 | 14200 | 2198 |
| 13 | 73712 | 11628 |
| 14 | 365596 | 62427 |
| 15 | 2279184 | 410701 |
Birçok çözüm yalnızca diğerlerinin dönmelerinden ibarettir ve simetri adı verilen bir tekniktir kesme özelliği gereken hesaplama miktarını azaltmak için kullanılabilir. Kullanma burada; Yukarıdaki çözüm hızlı olmayı değil, yalnızca basitliği kapsamayı amaçlamaktadır. Tabii ki yerine tek bir çözüm bulabilmeyi isteseydik çok daha hızlı yapabilirdik 50'ye kadar olan pano boyutları için en fazla birkaç milisaniye.
