MIP 문제 해결

다음 섹션에서는 MIP 문제의 예와 이를 해결하는 방법을 보여줍니다. 문제는 다음과 같습니다.

다음 제약 조건에 따라 x + 10y를 최대화합니다.

1. x + 7y ≤ 17.5
2. 0 ≤ x ≤ 3.5
3. 0 ≤ y
4. x, 정수 y개

제약 조건이 선형이므로 이는 선형 최적화 문제일 뿐이며, 이 경우 해가 정수여야 합니다. 아래 그래프는 문제에 가능한 영역의 정수 포인트를 보여줍니다.

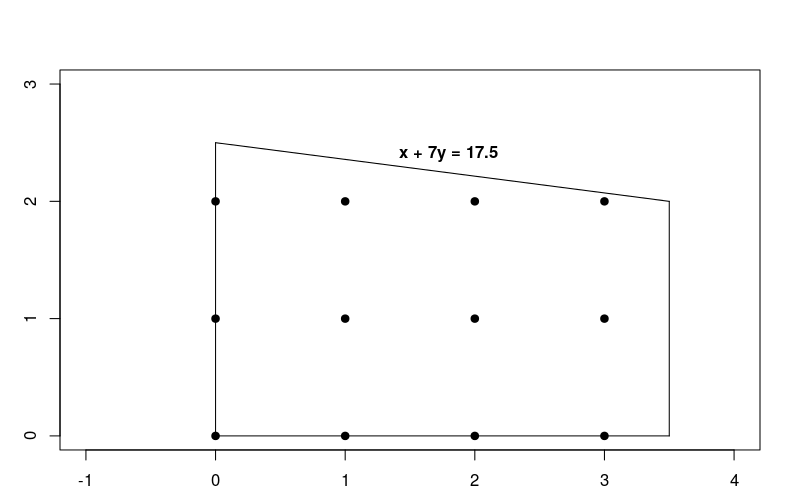
이 문제는 LP 문제 해결에 설명된 선형 최적화 문제와 매우 유사하지만 이 경우에는 해가 정수여야 합니다.

MIP 문제 해결을 위한 기본 단계

MIP 문제를 해결하려면 프로그램에 다음 단계가 포함되어야 합니다.

1. 선형 솔버 래퍼를 가져옵니다.
2. MIP 솔버를 선언하면
3. 변수를 정의하고
4. 제약 조건을 정의하고
5. 목표를 정의하고
6. MIP 솔버를 호출하고
7. 솔루션 표시

MPSolver를 사용하는 솔루션

다음 섹션에서는 MPSolver 래퍼와 MIP 솔버를 사용하여 문제를 해결하는 프로그램을 보여줍니다.

참고: 아래 프로그램을 실행하려면 OR-Tools를 설치해야 합니다.

기본 OR-도구 MIP 솔버는 SCIP입니다.

선형 솔버 래퍼 가져오기

아래와 같이 MIP 솔버 및 선형 솔버용 인터페이스인 OR-Tools 선형 솔버 래퍼를 가져오거나 포함합니다.

Python

from ortools.linear_solver import pywraplp

C++

#include <memory>

#include "ortools/linear_solver/linear_solver.h"

Java

import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;

C#

using System;
using Google.OrTools.LinearSolver;

MIP 솔버 선언

다음 코드는 문제의 MIP 솔버를 선언합니다. 이 예에서는 타사 솔버 SCIP를 사용합니다.

참고: 소스에서 OR-도구를 빌드하고 다른 해결자를 설치하고 사용하려면 플랫폼별 설치 가이드를 참고하세요.

Python

# Create the mip solver with the SCIP backend.
solver = pywraplp.Solver.CreateSolver("SAT")
if not solver:
    return

C++

// Create the mip solver with the SCIP backend.
std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
if (!solver) {
  LOG(WARNING) << "SCIP solver unavailable.";
  return;
}

Java

// Create the linear solver with the SCIP backend.
MPSolver solver = MPSolver.createSolver("SCIP");
if (solver == null) {
  System.out.println("Could not create solver SCIP");
  return;
}

C#

// Create the linear solver with the SCIP backend.
Solver solver = Solver.CreateSolver("SCIP");
if (solver is null)
{
    return;
}

변수 정의

다음 코드는 문제의 변수를 정의합니다.

Python

infinity = solver.infinity()
# x and y are integer non-negative variables.
x = solver.IntVar(0.0, infinity, "x")
y = solver.IntVar(0.0, infinity, "y")

print("Number of variables =", solver.NumVariables())

C++

const double infinity = solver->infinity();
// x and y are integer non-negative variables.
MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x");
MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y");

LOG(INFO) << "Number of variables = " << solver->NumVariables();

Java

double infinity = java.lang.Double.POSITIVE_INFINITY;
// x and y are integer non-negative variables.
MPVariable x = solver.makeIntVar(0.0, infinity, "x");
MPVariable y = solver.makeIntVar(0.0, infinity, "y");

System.out.println("Number of variables = " + solver.numVariables());

C#

// x and y are integer non-negative variables.
Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x");
Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y");

Console.WriteLine("Number of variables = " + solver.NumVariables());

프로그램은 MakeIntVar 메서드 (또는 코딩 언어에 따라 변형)를 사용하여 음수가 아닌 정수 값을 사용하는 x 및 y 변수를 만듭니다.

제약조건 정의

다음 코드는 문제의 제약 조건을 정의합니다.

Python

# x + 7 * y <= 17.5.
solver.Add(x + 7 * y <= 17.5)

# x <= 3.5.
solver.Add(x <= 3.5)

print("Number of constraints =", solver.NumConstraints())

C++

// x + 7 * y <= 17.5.
MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 17.5, "c0");
c0->SetCoefficient(x, 1);
c0->SetCoefficient(y, 7);

// x <= 3.5.
MPConstraint* const c1 = solver->MakeRowConstraint(-infinity, 3.5, "c1");
c1->SetCoefficient(x, 1);
c1->SetCoefficient(y, 0);

LOG(INFO) << "Number of constraints = " << solver->NumConstraints();

Java

// x + 7 * y <= 17.5.
MPConstraint c0 = solver.makeConstraint(-infinity, 17.5, "c0");
c0.setCoefficient(x, 1);
c0.setCoefficient(y, 7);

// x <= 3.5.
MPConstraint c1 = solver.makeConstraint(-infinity, 3.5, "c1");
c1.setCoefficient(x, 1);
c1.setCoefficient(y, 0);

System.out.println("Number of constraints = " + solver.numConstraints());

C#

// x + 7 * y <= 17.5.
solver.Add(x + 7 * y <= 17.5);

// x <= 3.5.
solver.Add(x <= 3.5);

Console.WriteLine("Number of constraints = " + solver.NumConstraints());

목표 정의

다음 코드는 문제의 objective function를 정의합니다.

Python

# Maximize x + 10 * y.
solver.Maximize(x + 10 * y)

C++

// Maximize x + 10 * y.
MPObjective* const objective = solver->MutableObjective();
objective->SetCoefficient(x, 1);
objective->SetCoefficient(y, 10);
objective->SetMaximization();

Java

// Maximize x + 10 * y.
MPObjective objective = solver.objective();
objective.setCoefficient(x, 1);
objective.setCoefficient(y, 10);
objective.setMaximization();

C#

// Maximize x + 10 * y.
solver.Maximize(x + 10 * y);

문제 해결사 호출

다음 코드는 솔버를 호출합니다.

Python

print(f"Solving with {solver.SolverVersion()}")
status = solver.Solve()

C++

const MPSolver::ResultStatus result_status = solver->Solve();
// Check that the problem has an optimal solution.
if (result_status != MPSolver::OPTIMAL) {
  LOG(FATAL) << "The problem does not have an optimal solution!";
}

Java

final MPSolver.ResultStatus resultStatus = solver.solve();

C#

Solver.ResultStatus resultStatus = solver.Solve();

솔루션 표시

다음 코드는 솔루션을 보여줍니다.

Python

if status == pywraplp.Solver.OPTIMAL:
    print("Solution:")
    print("Objective value =", solver.Objective().Value())
    print("x =", x.solution_value())
    print("y =", y.solution_value())
else:
    print("The problem does not have an optimal solution.")

C++

LOG(INFO) << "Solution:";
LOG(INFO) << "Objective value = " << objective->Value();
LOG(INFO) << "x = " << x->solution_value();
LOG(INFO) << "y = " << y->solution_value();

Java

if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
  System.out.println("Solution:");
  System.out.println("Objective value = " + objective.value());
  System.out.println("x = " + x.solutionValue());
  System.out.println("y = " + y.solutionValue());
} else {
  System.err.println("The problem does not have an optimal solution!");
}

C#

// Check that the problem has an optimal solution.
if (resultStatus != Solver.ResultStatus.OPTIMAL)
{
    Console.WriteLine("The problem does not have an optimal solution!");
    return;
}
Console.WriteLine("Solution:");
Console.WriteLine("Objective value = " + solver.Objective().Value());
Console.WriteLine("x = " + x.SolutionValue());
Console.WriteLine("y = " + y.SolutionValue());

이 문제의 해결 방법은 다음과 같습니다.

Number of variables = 2
Number of constraints = 2
Solution:
Objective value = 23
x = 3
y = 2

목표 함수의 최적 값은 23이며 x = 3, y = 2 지점에서 발생합니다.

프로그램 이수

전체 프로그램은 다음과 같습니다.

Python

from ortools.linear_solver import pywraplp


def main():
    # Create the mip solver with the SCIP backend.
    solver = pywraplp.Solver.CreateSolver("SAT")
    if not solver:
        return

    infinity = solver.infinity()
    # x and y are integer non-negative variables.
    x = solver.IntVar(0.0, infinity, "x")
    y = solver.IntVar(0.0, infinity, "y")

    print("Number of variables =", solver.NumVariables())

    # x + 7 * y <= 17.5.
    solver.Add(x + 7 * y <= 17.5)

    # x <= 3.5.
    solver.Add(x <= 3.5)

    print("Number of constraints =", solver.NumConstraints())

    # Maximize x + 10 * y.
    solver.Maximize(x + 10 * y)

    print(f"Solving with {solver.SolverVersion()}")
    status = solver.Solve()

    if status == pywraplp.Solver.OPTIMAL:
        print("Solution:")
        print("Objective value =", solver.Objective().Value())
        print("x =", x.solution_value())
        print("y =", y.solution_value())
    else:
        print("The problem does not have an optimal solution.")

    print("\nAdvanced usage:")
    print(f"Problem solved in {solver.wall_time():d} milliseconds")
    print(f"Problem solved in {solver.iterations():d} iterations")
    print(f"Problem solved in {solver.nodes():d} branch-and-bound nodes")


if __name__ == "__main__":
    main()

C++

#include <memory>

#include "ortools/linear_solver/linear_solver.h"

namespace operations_research {
void SimpleMipProgram() {
  // Create the mip solver with the SCIP backend.
  std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
  if (!solver) {
    LOG(WARNING) << "SCIP solver unavailable.";
    return;
  }

  const double infinity = solver->infinity();
  // x and y are integer non-negative variables.
  MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x");
  MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y");

  LOG(INFO) << "Number of variables = " << solver->NumVariables();

  // x + 7 * y <= 17.5.
  MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 17.5, "c0");
  c0->SetCoefficient(x, 1);
  c0->SetCoefficient(y, 7);

  // x <= 3.5.
  MPConstraint* const c1 = solver->MakeRowConstraint(-infinity, 3.5, "c1");
  c1->SetCoefficient(x, 1);
  c1->SetCoefficient(y, 0);

  LOG(INFO) << "Number of constraints = " << solver->NumConstraints();

  // Maximize x + 10 * y.
  MPObjective* const objective = solver->MutableObjective();
  objective->SetCoefficient(x, 1);
  objective->SetCoefficient(y, 10);
  objective->SetMaximization();

  const MPSolver::ResultStatus result_status = solver->Solve();
  // Check that the problem has an optimal solution.
  if (result_status != MPSolver::OPTIMAL) {
    LOG(FATAL) << "The problem does not have an optimal solution!";
  }

  LOG(INFO) << "Solution:";
  LOG(INFO) << "Objective value = " << objective->Value();
  LOG(INFO) << "x = " << x->solution_value();
  LOG(INFO) << "y = " << y->solution_value();

  LOG(INFO) << "\nAdvanced usage:";
  LOG(INFO) << "Problem solved in " << solver->wall_time() << " milliseconds";
  LOG(INFO) << "Problem solved in " << solver->iterations() << " iterations";
  LOG(INFO) << "Problem solved in " << solver->nodes()
            << " branch-and-bound nodes";
}
}  // namespace operations_research

int main(int argc, char** argv) {
  operations_research::SimpleMipProgram();
  return EXIT_SUCCESS;
}

Java

package com.google.ortools.linearsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;

/** Minimal Mixed Integer Programming example to showcase calling the solver. */
public final class SimpleMipProgram {
  public static void main(String[] args) {
    Loader.loadNativeLibraries();
    // Create the linear solver with the SCIP backend.
    MPSolver solver = MPSolver.createSolver("SCIP");
    if (solver == null) {
      System.out.println("Could not create solver SCIP");
      return;
    }

    double infinity = java.lang.Double.POSITIVE_INFINITY;
    // x and y are integer non-negative variables.
    MPVariable x = solver.makeIntVar(0.0, infinity, "x");
    MPVariable y = solver.makeIntVar(0.0, infinity, "y");

    System.out.println("Number of variables = " + solver.numVariables());

    // x + 7 * y <= 17.5.
    MPConstraint c0 = solver.makeConstraint(-infinity, 17.5, "c0");
    c0.setCoefficient(x, 1);
    c0.setCoefficient(y, 7);

    // x <= 3.5.
    MPConstraint c1 = solver.makeConstraint(-infinity, 3.5, "c1");
    c1.setCoefficient(x, 1);
    c1.setCoefficient(y, 0);

    System.out.println("Number of constraints = " + solver.numConstraints());

    // Maximize x + 10 * y.
    MPObjective objective = solver.objective();
    objective.setCoefficient(x, 1);
    objective.setCoefficient(y, 10);
    objective.setMaximization();

    final MPSolver.ResultStatus resultStatus = solver.solve();

    if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
      System.out.println("Solution:");
      System.out.println("Objective value = " + objective.value());
      System.out.println("x = " + x.solutionValue());
      System.out.println("y = " + y.solutionValue());
    } else {
      System.err.println("The problem does not have an optimal solution!");
    }

    System.out.println("\nAdvanced usage:");
    System.out.println("Problem solved in " + solver.wallTime() + " milliseconds");
    System.out.println("Problem solved in " + solver.iterations() + " iterations");
    System.out.println("Problem solved in " + solver.nodes() + " branch-and-bound nodes");
  }

  private SimpleMipProgram() {}
}

C#

using System;
using Google.OrTools.LinearSolver;

public class SimpleMipProgram
{
    static void Main()
    {
        // Create the linear solver with the SCIP backend.
        Solver solver = Solver.CreateSolver("SCIP");
        if (solver is null)
        {
            return;
        }

        // x and y are integer non-negative variables.
        Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x");
        Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y");

        Console.WriteLine("Number of variables = " + solver.NumVariables());

        // x + 7 * y <= 17.5.
        solver.Add(x + 7 * y <= 17.5);

        // x <= 3.5.
        solver.Add(x <= 3.5);

        Console.WriteLine("Number of constraints = " + solver.NumConstraints());

        // Maximize x + 10 * y.
        solver.Maximize(x + 10 * y);

        Solver.ResultStatus resultStatus = solver.Solve();

        // Check that the problem has an optimal solution.
        if (resultStatus != Solver.ResultStatus.OPTIMAL)
        {
            Console.WriteLine("The problem does not have an optimal solution!");
            return;
        }
        Console.WriteLine("Solution:");
        Console.WriteLine("Objective value = " + solver.Objective().Value());
        Console.WriteLine("x = " + x.SolutionValue());
        Console.WriteLine("y = " + y.SolutionValue());

        Console.WriteLine("\nAdvanced usage:");
        Console.WriteLine("Problem solved in " + solver.WallTime() + " milliseconds");
        Console.WriteLine("Problem solved in " + solver.Iterations() + " iterations");
        Console.WriteLine("Problem solved in " + solver.Nodes() + " branch-and-bound nodes");
    }
}

선형 최적화와 정수 최적화 비교

이 해를 위에 표시된 정수 최적화 문제와, 정수 제약 조건이 제거된 해당 선형 최적화 문제의 해법을 비교해 보겠습니다. 정수 문제의 해결책은 선형 솔루션에 가장 가까운 가능한 영역, 즉 x = 0, y = 2의 정수 지점이라고 생각할 수 있습니다. 하지만 보시다시피 이는 사실이 아닙니다.

이전 섹션의 프로그램을 다음과 같이 변경하여 선형 문제를 해결할 수 있습니다.

• MIP 솔버 교체

  Python

  # Create the mip solver with the SCIP backend.
  solver = pywraplp.Solver.CreateSolver("SAT")
  if not solver:
      return

  C++

  // Create the mip solver with the SCIP backend.
  std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
  if (!solver) {
    LOG(WARNING) << "SCIP solver unavailable.";
    return;
  }

  Java

  // Create the linear solver with the SCIP backend.
  MPSolver solver = MPSolver.createSolver("SCIP");
  if (solver == null) {
    System.out.println("Could not create solver SCIP");
    return;
  }

  C#

  // Create the linear solver with the SCIP backend.
  Solver solver = Solver.CreateSolver("SCIP");
  if (solver is null)
  {
      return;
  }

  LP 솔버와 함께

  Python

  # Create the linear solver with the GLOP backend.
  solver = pywraplp.Solver.CreateSolver("GLOP")
  if not solver:
      return

  C++

  // Create the linear solver with the GLOP backend.
  std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("GLOP"));

  Java

  // Create the linear solver with the GLOP backend.
  MPSolver solver = MPSolver.createSolver("GLOP");
  if (solver == null) {
    System.out.println("Could not create solver SCIP");
    return;
  }

  C#

  // Create the linear solver with the GLOP backend.
  Solver solver = Solver.CreateSolver("GLOP");
  if (solver is null)
  {
      return;
  }

• 정수 변수 바꾸기

  Python

  infinity = solver.infinity()
  # x and y are integer non-negative variables.
  x = solver.IntVar(0.0, infinity, "x")
  y = solver.IntVar(0.0, infinity, "y")
  
  print("Number of variables =", solver.NumVariables())

  C++

  const double infinity = solver->infinity();
  // x and y are integer non-negative variables.
  MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x");
  MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y");
  
  LOG(INFO) << "Number of variables = " << solver->NumVariables();

  Java

  double infinity = java.lang.Double.POSITIVE_INFINITY;
  // x and y are integer non-negative variables.
  MPVariable x = solver.makeIntVar(0.0, infinity, "x");
  MPVariable y = solver.makeIntVar(0.0, infinity, "y");
  
  System.out.println("Number of variables = " + solver.numVariables());

  C#

  // x and y are integer non-negative variables.
  Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x");
  Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y");
  
  Console.WriteLine("Number of variables = " + solver.NumVariables());

  (연속 변수 사용)

  Python

  infinity = solver.infinity()
  # Create the variables x and y.
  x = solver.NumVar(0.0, infinity, "x")
  y = solver.NumVar(0.0, infinity, "y")
  
  print("Number of variables =", solver.NumVariables())

  C++

  const double infinity = solver->infinity();
  // Create the variables x and y.
  MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x");
  MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y");
  
  LOG(INFO) << "Number of variables = " << solver->NumVariables();

  Java

  double infinity = java.lang.Double.POSITIVE_INFINITY;
  // Create the variables x and y.
  MPVariable x = solver.makeNumVar(0.0, infinity, "x");
  MPVariable y = solver.makeNumVar(0.0, infinity, "y");
  
  System.out.println("Number of variables = " + solver.numVariables());

  C#

  // Create the variables x and y.
  Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x");
  Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y");
  
  Console.WriteLine("Number of variables = " + solver.NumVariables());

이렇게 변경하고 프로그램을 다시 실행하면 다음과 같은 출력이 표시됩니다.

Number of variables = 2
Number of constraints = 2
Objective value = 25.000000
x = 0.000000
y = 2.500000

선형 문제의 해법은 목표 함수가 25인 x = 0, y = 2.5 지점에서 발생합니다. 이 그래프는 선형 문제와 정수 문제에 대한 해결책을 보여줍니다.

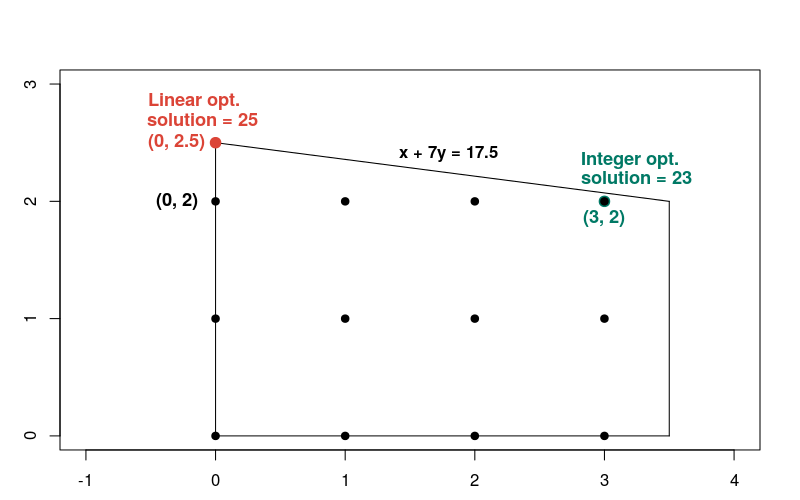
이 정수 해는 가능한 리전의 다른 정수 포인트와 비교할 때 선형 해법과 가깝지 않습니다. 일반적으로 선형 최적화 문제와 해당 정수 최적화 문제의 해결책은 서로 크게 다를 수 있습니다. 따라서 두 유형의 문제에는 서로 다른 해결 방법이 필요합니다.