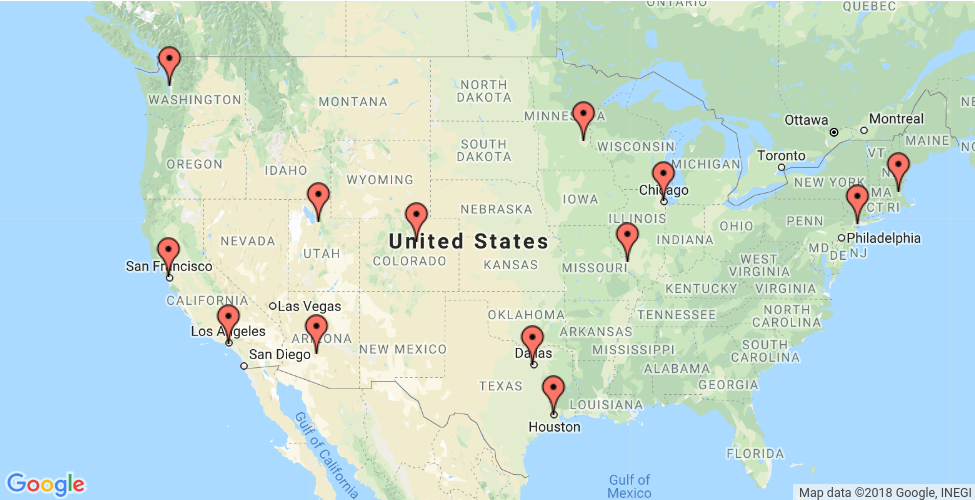
En esta sección, se presenta un ejemplo en el que se muestra cómo resolver el problema del viajante (TSP) de las ubicaciones que aparecen en el mapa a continuación.
En las siguientes secciones, se presentan programas en Python, C++, Java y C# que resuelven el TSP mediante el uso de las herramientas de OR.
Crea los datos
El siguiente código crea los datos para el problema.
Python
def create_data_model():
"""Stores the data for the problem."""
data = {}
data["distance_matrix"] = [
[0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972],
[2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579],
[713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260],
[1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987],
[1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371],
[1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999],
[2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701],
[213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099],
[2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600],
[875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162],
[1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200],
[2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504],
[1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0],
]
data["num_vehicles"] = 1
data["depot"] = 0
return data
C++
struct DataModel {
const std::vector<std::vector<int64_t>> distance_matrix{
{0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972},
{2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579},
{713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260},
{1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987},
{1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371},
{1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999},
{2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701},
{213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099},
{2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600},
{875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162},
{1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200},
{2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504},
{1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0},
};
const int num_vehicles = 1;
const RoutingIndexManager::NodeIndex depot{0};
};
Java
static class DataModel {
public final long[][] distanceMatrix = {
{0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972},
{2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579},
{713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260},
{1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987},
{1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371},
{1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999},
{2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701},
{213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099},
{2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600},
{875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162},
{1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200},
{2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504},
{1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0},
};
public final int vehicleNumber = 1;
public final int depot = 0;
}
C#
class DataModel
{
public long[,] DistanceMatrix = {
{ 0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972 },
{ 2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579 },
{ 713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260 },
{ 1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987 },
{ 1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371 },
{ 1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999 },
{ 2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701 },
{ 213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099 },
{ 2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600 },
{ 875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162 },
{ 1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200 },
{ 2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504 },
{ 1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0 },
};
public int VehicleNumber = 1;
public int Depot = 0;
};
La matriz de distancia es un arreglo cuya entrada i, j es la distancia desde la ubicación i hasta la ubicación j en millas, donde los índices del arreglo corresponden a las ubicaciones en el siguiente orden:
0. New York - 1. Los Angeles - 2. Chicago - 3. Minneapolis - 4. Denver - 5. Dallas
- 6. Seattle - 7. Boston - 8. San Francisco - 9. St. Louis - 10. Houston - 11. Phoenix - 12. Salt Lake City
Los datos también incluyen lo siguiente:
- La cantidad de vehículos en el problema, que es 1 porque es un TSP (En el caso de un problema de enrutamiento del vehículo, el número de vehículos puede ser mayor que 1).
- El depósito: Las ubicaciones de inicio y fin de la ruta. En este caso, el depósito es 0, que corresponde a Nueva York.
Otras formas de crear la matriz de distancia
En este ejemplo, la matriz de distancia se define de forma explícita en el programa. También es posible usar una función para calcular distancias entre ubicaciones: por ejemplo, la fórmula euclidiana para la distancia entre puntos en el plano. Sin embargo, aún es más eficiente calcular con anterioridad todas las distancias entre las ubicaciones y almacenarlas en una matriz, en lugar de calcularlas en el tiempo de ejecución. Consulta Ejemplo: perforar una placa de circuito para ver un ejemplo que crea la matriz de distancia de esta manera.
Otra alternativa es usar la API de Distance Matrix de Google Maps a fin de crear de forma dinámica una matriz de distancia (o tiempo de viaje) para un problema de enrutamiento.
Crea el modelo de enrutamiento
Con el siguiente código en la sección principal de los programas, se crea el administrador de índice (manager) y el modelo de enrutamiento (routing). El método manager.IndexToNode convierte los índices del agente de resolución (que puedes ignorar de forma segura) en los números de las ubicaciones. Los números de ubicación corresponden a los índices de la matriz de distancia.
Python
data = create_data_model()
manager = pywrapcp.RoutingIndexManager(
len(data["distance_matrix"]), data["num_vehicles"], data["depot"]
)
routing = pywrapcp.RoutingModel(manager)
C++
DataModel data;
RoutingIndexManager manager(data.distance_matrix.size(), data.num_vehicles,
data.depot);
RoutingModel routing(manager);
Java
final DataModel data = new DataModel();
RoutingIndexManager manager =
new RoutingIndexManager(data.distanceMatrix.length, data.vehicleNumber, data.depot);
RoutingModel routing = new RoutingModel(manager);
C#
DataModel data = new DataModel();
RoutingIndexManager manager =
new RoutingIndexManager(data.DistanceMatrix.GetLength(0), data.VehicleNumber, data.Depot);
RoutingModel routing = new RoutingModel(manager);
Las entradas a RoutingIndexManager son las siguientes:
- La cantidad de filas de la matriz de distancia, que es el número de ubicaciones (incluido el depósito).
- La cantidad de vehículos en el problema
- El nodo que corresponde al depósito.
Crea la devolución de llamada de distancia
Para usar el agente de resolución de enrutamiento, debes crear una devolución de llamada de distancia (o tránsito): una función que tome cualquier par de ubicaciones y muestre la distancia entre ellas. La forma más sencilla de hacerlo es mediante la matriz de distancia.
La siguiente función crea la devolución de llamada y la registra con el agente de resolución como transit_callback_index.
Python
def distance_callback(from_index, to_index):
"""Returns the distance between the two nodes."""
# Convert from routing variable Index to distance matrix NodeIndex.
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return data["distance_matrix"][from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
C++
const int transit_callback_index = routing.RegisterTransitCallback(
[&data, &manager](const int64_t from_index,
const int64_t to_index) -> int64_t {
// Convert from routing variable Index to distance matrix NodeIndex.
const int from_node = manager.IndexToNode(from_index).value();
const int to_node = manager.IndexToNode(to_index).value();
return data.distance_matrix[from_node][to_node];
});
Java
final int transitCallbackIndex =
routing.registerTransitCallback((long fromIndex, long toIndex) -> {
// Convert from routing variable Index to user NodeIndex.
int fromNode = manager.indexToNode(fromIndex);
int toNode = manager.indexToNode(toIndex);
return data.distanceMatrix[fromNode][toNode];
});
C#
int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
{
// Convert from routing variable Index to
// distance matrix NodeIndex.
var fromNode = manager.IndexToNode(fromIndex);
var toNode = manager.IndexToNode(toIndex);
return data.DistanceMatrix[fromNode, toNode];
});
The callback accepts two indices, from_index and to_index, and returns the
corresponding entry of the distance matrix.
Set the cost of travel
The arc cost evaluator tells the solver how to calculate the cost of travel between any two locations — in other words, the cost of the edge (or arc) joining them in the graph for the problem. The following code sets the arc cost evaluator.
Python
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
C++
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
Java
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
C#
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
En este ejemplo, el evaluador de costo de arco es el transit_callback_index, que es la referencia interna del solucionador a la devolución de llamada de distancia. Esto significa que el costo de viaje entre dos ubicaciones es solo la distancia entre ellas.
Sin embargo, en general, los costos también pueden incluir otros factores.
También puedes usar el método routing.SetArcCostEvaluatorOfVehicle() para definir varios evaluadores de costos en arco que dependan del vehículo que viaja entre ubicaciones.
Por ejemplo, si los vehículos tienen velocidades diferentes, podrías definir el costo de viaje entre ubicaciones para que sea la distancia dividida por la velocidad del vehículo; en otras palabras, el tiempo de viaje.
Establecer parámetros de búsqueda
El siguiente código establece los parámetros de búsqueda predeterminados y un método heurístico para encontrar la primera solución:
Python
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC
)
C++
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
searchParameters.set_first_solution_strategy(
FirstSolutionStrategy::PATH_CHEAPEST_ARC);
Java
RoutingSearchParameters searchParameters =
main.defaultRoutingSearchParameters()
.toBuilder()
.setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
.build();
C#
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
El código establece la primera estrategia de solución en PATH_CHEAPEST_ARC, que crea una ruta inicial para la resolución de problemas mediante la adición repetida de bordes con el menor peso que no conduce a un nodo visitado con anterioridad (que no sea el depósito). Para ver otras opciones, consulta Estrategia de primera solución.
Agregar la impresora de la solución
A continuación, se muestra la función que muestra la solución que muestra el solucionador. La función extrae la ruta de la solución y la imprime en la consola.
Python
def print_solution(manager, routing, solution):
"""Prints solution on console."""
print(f"Objective: {solution.ObjectiveValue()} miles")
index = routing.Start(0)
plan_output = "Route for vehicle 0:\n"
route_distance = 0
while not routing.IsEnd(index):
plan_output += f" {manager.IndexToNode(index)} ->"
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(previous_index, index, 0)
plan_output += f" {manager.IndexToNode(index)}\n"
print(plan_output)
plan_output += f"Route distance: {route_distance}miles\n"
C++
//! @brief Print the solution.
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const RoutingIndexManager& manager,
const RoutingModel& routing, const Assignment& solution) {
// Inspect solution.
LOG(INFO) << "Objective: " << solution.ObjectiveValue() << " miles";
int64_t index = routing.Start(0);
LOG(INFO) << "Route:";
int64_t distance{0};
std::stringstream route;
while (!routing.IsEnd(index)) {
route << manager.IndexToNode(index).value() << " -> ";
const int64_t previous_index = index;
index = solution.Value(routing.NextVar(index));
distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0});
}
LOG(INFO) << route.str() << manager.IndexToNode(index).value();
LOG(INFO) << "Route distance: " << distance << "miles";
LOG(INFO) << "";
LOG(INFO) << "Advanced usage:";
LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}
Java
/// @brief Print the solution.
static void printSolution(
RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
// Solution cost.
logger.info("Objective: " + solution.objectiveValue() + "miles");
// Inspect solution.
logger.info("Route:");
long routeDistance = 0;
String route = "";
long index = routing.start(0);
while (!routing.isEnd(index)) {
route += manager.indexToNode(index) + " -> ";
long previousIndex = index;
index = solution.value(routing.nextVar(index));
routeDistance += routing.getArcCostForVehicle(previousIndex, index, 0);
}
route += manager.indexToNode(routing.end(0));
logger.info(route);
logger.info("Route distance: " + routeDistance + "miles");
}
C#
/// <summary>
/// Print the solution.
/// </summary>
static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution)
{
Console.WriteLine("Objective: {0} miles", solution.ObjectiveValue());
// Inspect solution.
Console.WriteLine("Route:");
long routeDistance = 0;
var index = routing.Start(0);
while (routing.IsEnd(index) == false)
{
Console.Write("{0} -> ", manager.IndexToNode((int)index));
var previousIndex = index;
index = solution.Value(routing.NextVar(index));
routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0);
}
Console.WriteLine("{0}", manager.IndexToNode((int)index));
Console.WriteLine("Route distance: {0}miles", routeDistance);
}
La función muestra la ruta óptima y su distancia, que proporciona ObjectiveValue().
Resolver e imprimir la solución
Por último, puedes llamar al agente de resolución y, luego, imprimir la solución:
Python
solution = routing.SolveWithParameters(search_parameters)
if solution:
print_solution(manager, routing, solution)
C++
const Assignment* solution = routing.SolveWithParameters(searchParameters); PrintSolution(manager, routing, *solution);
Java
Assignment solution = routing.solveWithParameters(searchParameters); printSolution(routing, manager, solution);
C#
Assignment solution = routing.SolveWithParameters(searchParameters); PrintSolution(routing, manager, solution);
Esto muestra la solución y muestra la ruta óptima.
Ejecuta los programas
Cuando ejecutas los programas, se muestra el siguiente resultado.
Objective: 7293 miles Route for vehicle 0: 0 -> 7 -> 2 -> 3 -> 4 -> 12 -> 6 -> 8 -> 1 -> 11 -> 10 -> 5 -> 9 -> 0
En este ejemplo, solo hay una ruta porque es un TSP. Sin embargo, en los problemas de enrutamiento de vehículos más generales, la solución contiene varias rutas.
Cómo guardar rutas en una lista o un arreglo
Como alternativa a imprimir directamente la solución, puedes guardar la ruta (o rutas, para un VRP) en una lista o arreglo. Esto tiene la ventaja de que las rutas están disponibles en caso de que quieras hacer algo con ellas más tarde. Por ejemplo, puedes ejecutar el programa varias veces con diferentes parámetros y guardar las rutas en las soluciones mostradas en un archivo para compararlas.
Las siguientes funciones guardan las rutas de la solución en cualquier VRP (posiblemente con varios vehículos) como una lista (Python) o un arreglo (C++).
Python
def get_routes(solution, routing, manager):
"""Get vehicle routes from a solution and store them in an array."""
# Get vehicle routes and store them in a two dimensional array whose
# i,j entry is the jth location visited by vehicle i along its route.
routes = []
for route_nbr in range(routing.vehicles()):
index = routing.Start(route_nbr)
route = [manager.IndexToNode(index)]
while not routing.IsEnd(index):
index = solution.Value(routing.NextVar(index))
route.append(manager.IndexToNode(index))
routes.append(route)
return routes
C++
std::vector<std::vector<int>> GetRoutes(const Assignment& solution,
const RoutingModel& routing,
const RoutingIndexManager& manager) {
// Get vehicle routes and store them in a two dimensional array, whose
// i, j entry is the node for the jth visit of vehicle i.
std::vector<std::vector<int>> routes(manager.num_vehicles());
// Get routes.
for (int vehicle_id = 0; vehicle_id < manager.num_vehicles(); ++vehicle_id) {
int64_t index = routing.Start(vehicle_id);
routes[vehicle_id].push_back(manager.IndexToNode(index).value());
while (!routing.IsEnd(index)) {
index = solution.Value(routing.NextVar(index));
routes[vehicle_id].push_back(manager.IndexToNode(index).value());
}
}
return routes;
}
Puedes usar estas funciones para obtener las rutas en cualquiera de los ejemplos de VRP en la sección Enrutamiento.
En el siguiente código, se muestran las rutas.
Python
routes = get_routes(solution, routing, manager)
# Display the routes.
for i, route in enumerate(routes):
print('Route', i, route)
C++
const std::vector⟨std::vector⟨int⟩⟩
routes = GetRoutes(*solution,
routing,
manager);
// Display the routes.
for (int vehicle_id = 0; vehicle_id < routes.size(); ++vehicle_id) {
LOG(INFO) << "Route " << vehicle_id;
for (int j = 1; j < routes[vehicle_id].size(); ++j) {
LOG(INFO) << routes[vehicle_id][j];
}
}
Para el ejemplo actual, este código muestra la siguiente ruta:
Route 0 [0, 7, 2, 3, 4, 12, 6, 8, 1, 11, 10, 5, 9, 0]
Como ejercicio, modifica el código anterior a fin de dar formato al resultado de la misma manera que la impresora de solución para el programa.
Programas completos
Los programas TSP completos se muestran a continuación.
Python
"""Simple Travelling Salesperson Problem (TSP) between cities."""
from ortools.constraint_solver import routing_enums_pb2
from ortools.constraint_solver import pywrapcp
def create_data_model():
"""Stores the data for the problem."""
data = {}
data["distance_matrix"] = [
[0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972],
[2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579],
[713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260],
[1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987],
[1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371],
[1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999],
[2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701],
[213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099],
[2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600],
[875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162],
[1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200],
[2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504],
[1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0],
]
data["num_vehicles"] = 1
data["depot"] = 0
return data
def print_solution(manager, routing, solution):
"""Prints solution on console."""
print(f"Objective: {solution.ObjectiveValue()} miles")
index = routing.Start(0)
plan_output = "Route for vehicle 0:\n"
route_distance = 0
while not routing.IsEnd(index):
plan_output += f" {manager.IndexToNode(index)} ->"
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(previous_index, index, 0)
plan_output += f" {manager.IndexToNode(index)}\n"
print(plan_output)
plan_output += f"Route distance: {route_distance}miles\n"
def main():
"""Entry point of the program."""
# Instantiate the data problem.
data = create_data_model()
# Create the routing index manager.
manager = pywrapcp.RoutingIndexManager(
len(data["distance_matrix"]), data["num_vehicles"], data["depot"]
)
# Create Routing Model.
routing = pywrapcp.RoutingModel(manager)
def distance_callback(from_index, to_index):
"""Returns the distance between the two nodes."""
# Convert from routing variable Index to distance matrix NodeIndex.
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return data["distance_matrix"][from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
# Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
# Setting first solution heuristic.
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC
)
# Solve the problem.
solution = routing.SolveWithParameters(search_parameters)
# Print solution on console.
if solution:
print_solution(manager, routing, solution)
if __name__ == "__main__":
main()
C++
#include <cmath>
#include <cstdint>
#include <sstream>
#include <vector>
#include "ortools/constraint_solver/routing.h"
#include "ortools/constraint_solver/routing_enums.pb.h"
#include "ortools/constraint_solver/routing_index_manager.h"
#include "ortools/constraint_solver/routing_parameters.h"
namespace operations_research {
struct DataModel {
const std::vector<std::vector<int64_t>> distance_matrix{
{0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972},
{2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579},
{713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260},
{1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987},
{1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371},
{1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999},
{2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701},
{213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099},
{2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600},
{875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162},
{1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200},
{2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504},
{1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0},
};
const int num_vehicles = 1;
const RoutingIndexManager::NodeIndex depot{0};
};
//! @brief Print the solution.
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const RoutingIndexManager& manager,
const RoutingModel& routing, const Assignment& solution) {
// Inspect solution.
LOG(INFO) << "Objective: " << solution.ObjectiveValue() << " miles";
int64_t index = routing.Start(0);
LOG(INFO) << "Route:";
int64_t distance{0};
std::stringstream route;
while (!routing.IsEnd(index)) {
route << manager.IndexToNode(index).value() << " -> ";
const int64_t previous_index = index;
index = solution.Value(routing.NextVar(index));
distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0});
}
LOG(INFO) << route.str() << manager.IndexToNode(index).value();
LOG(INFO) << "Route distance: " << distance << "miles";
LOG(INFO) << "";
LOG(INFO) << "Advanced usage:";
LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}
void Tsp() {
// Instantiate the data problem.
DataModel data;
// Create Routing Index Manager
RoutingIndexManager manager(data.distance_matrix.size(), data.num_vehicles,
data.depot);
// Create Routing Model.
RoutingModel routing(manager);
const int transit_callback_index = routing.RegisterTransitCallback(
[&data, &manager](const int64_t from_index,
const int64_t to_index) -> int64_t {
// Convert from routing variable Index to distance matrix NodeIndex.
const int from_node = manager.IndexToNode(from_index).value();
const int to_node = manager.IndexToNode(to_index).value();
return data.distance_matrix[from_node][to_node];
});
// Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
searchParameters.set_first_solution_strategy(
FirstSolutionStrategy::PATH_CHEAPEST_ARC);
// Solve the problem.
const Assignment* solution = routing.SolveWithParameters(searchParameters);
// Print solution on console.
PrintSolution(manager, routing, *solution);
}
} // namespace operations_research
int main(int /*argc*/, char* /*argv*/[]) {
operations_research::Tsp();
return EXIT_SUCCESS;
}
Java
package com.google.ortools.constraintsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.Assignment;
import com.google.ortools.constraintsolver.FirstSolutionStrategy;
import com.google.ortools.constraintsolver.RoutingIndexManager;
import com.google.ortools.constraintsolver.RoutingModel;
import com.google.ortools.constraintsolver.RoutingSearchParameters;
import com.google.ortools.constraintsolver.main;
import java.util.logging.Logger;
/** Minimal TSP using distance matrix. */
public class TspCities {
private static final Logger logger = Logger.getLogger(TspCities.class.getName());
static class DataModel {
public final long[][] distanceMatrix = {
{0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972},
{2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579},
{713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260},
{1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987},
{1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371},
{1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999},
{2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701},
{213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099},
{2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600},
{875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162},
{1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200},
{2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504},
{1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0},
};
public final int vehicleNumber = 1;
public final int depot = 0;
}
/// @brief Print the solution.
static void printSolution(
RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
// Solution cost.
logger.info("Objective: " + solution.objectiveValue() + "miles");
// Inspect solution.
logger.info("Route:");
long routeDistance = 0;
String route = "";
long index = routing.start(0);
while (!routing.isEnd(index)) {
route += manager.indexToNode(index) + " -> ";
long previousIndex = index;
index = solution.value(routing.nextVar(index));
routeDistance += routing.getArcCostForVehicle(previousIndex, index, 0);
}
route += manager.indexToNode(routing.end(0));
logger.info(route);
logger.info("Route distance: " + routeDistance + "miles");
}
public static void main(String[] args) throws Exception {
Loader.loadNativeLibraries();
// Instantiate the data problem.
final DataModel data = new DataModel();
// Create Routing Index Manager
RoutingIndexManager manager =
new RoutingIndexManager(data.distanceMatrix.length, data.vehicleNumber, data.depot);
// Create Routing Model.
RoutingModel routing = new RoutingModel(manager);
// Create and register a transit callback.
final int transitCallbackIndex =
routing.registerTransitCallback((long fromIndex, long toIndex) -> {
// Convert from routing variable Index to user NodeIndex.
int fromNode = manager.indexToNode(fromIndex);
int toNode = manager.indexToNode(toIndex);
return data.distanceMatrix[fromNode][toNode];
});
// Define cost of each arc.
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters =
main.defaultRoutingSearchParameters()
.toBuilder()
.setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
.build();
// Solve the problem.
Assignment solution = routing.solveWithParameters(searchParameters);
// Print solution on console.
printSolution(routing, manager, solution);
}
}
C#
using System;
using System.Collections.Generic;
using Google.OrTools.ConstraintSolver;
/// <summary>
/// Minimal TSP using distance matrix.
/// </summary>
public class TspCities
{
class DataModel
{
public long[,] DistanceMatrix = {
{ 0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972 },
{ 2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579 },
{ 713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260 },
{ 1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987 },
{ 1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371 },
{ 1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999 },
{ 2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701 },
{ 213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099 },
{ 2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600 },
{ 875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162 },
{ 1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200 },
{ 2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504 },
{ 1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0 },
};
public int VehicleNumber = 1;
public int Depot = 0;
};
/// <summary>
/// Print the solution.
/// </summary>
static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution)
{
Console.WriteLine("Objective: {0} miles", solution.ObjectiveValue());
// Inspect solution.
Console.WriteLine("Route:");
long routeDistance = 0;
var index = routing.Start(0);
while (routing.IsEnd(index) == false)
{
Console.Write("{0} -> ", manager.IndexToNode((int)index));
var previousIndex = index;
index = solution.Value(routing.NextVar(index));
routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0);
}
Console.WriteLine("{0}", manager.IndexToNode((int)index));
Console.WriteLine("Route distance: {0}miles", routeDistance);
}
public static void Main(String[] args)
{
// Instantiate the data problem.
DataModel data = new DataModel();
// Create Routing Index Manager
RoutingIndexManager manager =
new RoutingIndexManager(data.DistanceMatrix.GetLength(0), data.VehicleNumber, data.Depot);
// Create Routing Model.
RoutingModel routing = new RoutingModel(manager);
int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
{
// Convert from routing variable Index to
// distance matrix NodeIndex.
var fromNode = manager.IndexToNode(fromIndex);
var toNode = manager.IndexToNode(toIndex);
return data.DistanceMatrix[fromNode, toNode];
});
// Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
// Solve the problem.
Assignment solution = routing.SolveWithParameters(searchParameters);
// Print solution on console.
PrintSolution(routing, manager, solution);
}
}
Ejemplo: perforar una placa de circuito
En el siguiente ejemplo, se incluyen perforaciones en un panel de circuitos con un taladro automático. El problema es encontrar la ruta más corta para que el taladro tome en la placa y pueda perforar todos los agujeros requeridos. El ejemplo se toma de TSPLIB, una biblioteca de problemas de TSP.
A continuación, se muestra un gráfico de dispersión de las ubicaciones de los agujeros:
En las siguientes secciones, se presentan programas que encuentran una buena solución al problema de la placa de circuito mediante los parámetros de búsqueda predeterminados del solucionador. Luego, te mostraremos cómo encontrar una mejor solución mediante el cambio de la estrategia de búsqueda.
Crea los datos
Los datos del problema constan de 280 puntos en el plano, que se muestran en el gráfico de dispersión anterior. El programa crea los datos en un arreglo de pares ordenados que corresponden a los puntos en el plano, como se muestra a continuación.
Python
def create_data_model():
"""Stores the data for the problem."""
data = {}
# Locations in block units
data["locations"] = [
# fmt: off
(288, 149), (288, 129), (270, 133), (256, 141), (256, 157), (246, 157),
(236, 169), (228, 169), (228, 161), (220, 169), (212, 169), (204, 169),
(196, 169), (188, 169), (196, 161), (188, 145), (172, 145), (164, 145),
(156, 145), (148, 145), (140, 145), (148, 169), (164, 169), (172, 169),
(156, 169), (140, 169), (132, 169), (124, 169), (116, 161), (104, 153),
(104, 161), (104, 169), (90, 165), (80, 157), (64, 157), (64, 165),
(56, 169), (56, 161), (56, 153), (56, 145), (56, 137), (56, 129),
(56, 121), (40, 121), (40, 129), (40, 137), (40, 145), (40, 153),
(40, 161), (40, 169), (32, 169), (32, 161), (32, 153), (32, 145),
(32, 137), (32, 129), (32, 121), (32, 113), (40, 113), (56, 113),
(56, 105), (48, 99), (40, 99), (32, 97), (32, 89), (24, 89),
(16, 97), (16, 109), (8, 109), (8, 97), (8, 89), (8, 81),
(8, 73), (8, 65), (8, 57), (16, 57), (8, 49), (8, 41),
(24, 45), (32, 41), (32, 49), (32, 57), (32, 65), (32, 73),
(32, 81), (40, 83), (40, 73), (40, 63), (40, 51), (44, 43),
(44, 35), (44, 27), (32, 25), (24, 25), (16, 25), (16, 17),
(24, 17), (32, 17), (44, 11), (56, 9), (56, 17), (56, 25),
(56, 33), (56, 41), (64, 41), (72, 41), (72, 49), (56, 49),
(48, 51), (56, 57), (56, 65), (48, 63), (48, 73), (56, 73),
(56, 81), (48, 83), (56, 89), (56, 97), (104, 97), (104, 105),
(104, 113), (104, 121), (104, 129), (104, 137), (104, 145), (116, 145),
(124, 145), (132, 145), (132, 137), (140, 137), (148, 137), (156, 137),
(164, 137), (172, 125), (172, 117), (172, 109), (172, 101), (172, 93),
(172, 85), (180, 85), (180, 77), (180, 69), (180, 61), (180, 53),
(172, 53), (172, 61), (172, 69), (172, 77), (164, 81), (148, 85),
(124, 85), (124, 93), (124, 109), (124, 125), (124, 117), (124, 101),
(104, 89), (104, 81), (104, 73), (104, 65), (104, 49), (104, 41),
(104, 33), (104, 25), (104, 17), (92, 9), (80, 9), (72, 9),
(64, 21), (72, 25), (80, 25), (80, 25), (80, 41), (88, 49),
(104, 57), (124, 69), (124, 77), (132, 81), (140, 65), (132, 61),
(124, 61), (124, 53), (124, 45), (124, 37), (124, 29), (132, 21),
(124, 21), (120, 9), (128, 9), (136, 9), (148, 9), (162, 9),
(156, 25), (172, 21), (180, 21), (180, 29), (172, 29), (172, 37),
(172, 45), (180, 45), (180, 37), (188, 41), (196, 49), (204, 57),
(212, 65), (220, 73), (228, 69), (228, 77), (236, 77), (236, 69),
(236, 61), (228, 61), (228, 53), (236, 53), (236, 45), (228, 45),
(228, 37), (236, 37), (236, 29), (228, 29), (228, 21), (236, 21),
(252, 21), (260, 29), (260, 37), (260, 45), (260, 53), (260, 61),
(260, 69), (260, 77), (276, 77), (276, 69), (276, 61), (276, 53),
(284, 53), (284, 61), (284, 69), (284, 77), (284, 85), (284, 93),
(284, 101), (288, 109), (280, 109), (276, 101), (276, 93), (276, 85),
(268, 97), (260, 109), (252, 101), (260, 93), (260, 85), (236, 85),
(228, 85), (228, 93), (236, 93), (236, 101), (228, 101), (228, 109),
(228, 117), (228, 125), (220, 125), (212, 117), (204, 109), (196, 101),
(188, 93), (180, 93), (180, 101), (180, 109), (180, 117), (180, 125),
(196, 145), (204, 145), (212, 145), (220, 145), (228, 145), (236, 145),
(246, 141), (252, 125), (260, 129), (280, 133)
# fmt: on
]
data["num_vehicles"] = 1
data["depot"] = 0
return data
C++
struct DataModel {
const std::vector<std::vector<int>> locations{
{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157}, {246, 157},
{236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169},
{196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145},
{156, 145}, {148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169},
{156, 169}, {140, 169}, {132, 169}, {124, 169}, {116, 161}, {104, 153},
{104, 161}, {104, 169}, {90, 165}, {80, 157}, {64, 157}, {64, 165},
{56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137}, {56, 129},
{56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153},
{40, 161}, {40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145},
{32, 137}, {32, 129}, {32, 121}, {32, 113}, {40, 113}, {56, 113},
{56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89}, {24, 89},
{16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81},
{8, 73}, {8, 65}, {8, 57}, {16, 57}, {8, 49}, {8, 41},
{24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65}, {32, 73},
{32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43},
{44, 35}, {44, 27}, {32, 25}, {24, 25}, {16, 25}, {16, 17},
{24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17}, {56, 25},
{56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49},
{48, 51}, {56, 57}, {56, 65}, {48, 63}, {48, 73}, {56, 73},
{56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97}, {104, 105},
{104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145},
{124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137},
{164, 137}, {172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93},
{172, 85}, {180, 85}, {180, 77}, {180, 69}, {180, 61}, {180, 53},
{172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81}, {148, 85},
{124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101},
{104, 89}, {104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41},
{104, 33}, {104, 25}, {104, 17}, {92, 9}, {80, 9}, {72, 9},
{64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49},
{104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61},
{124, 61}, {124, 53}, {124, 45}, {124, 37}, {124, 29}, {132, 21},
{124, 21}, {120, 9}, {128, 9}, {136, 9}, {148, 9}, {162, 9},
{156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37},
{172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57},
{212, 65}, {220, 73}, {228, 69}, {228, 77}, {236, 77}, {236, 69},
{236, 61}, {228, 61}, {228, 53}, {236, 53}, {236, 45}, {228, 45},
{228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21},
{252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61},
{260, 69}, {260, 77}, {276, 77}, {276, 69}, {276, 61}, {276, 53},
{284, 53}, {284, 61}, {284, 69}, {284, 77}, {284, 85}, {284, 93},
{284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85},
{268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85},
{228, 85}, {228, 93}, {236, 93}, {236, 101}, {228, 101}, {228, 109},
{228, 117}, {228, 125}, {220, 125}, {212, 117}, {204, 109}, {196, 101},
{188, 93}, {180, 93}, {180, 101}, {180, 109}, {180, 117}, {180, 125},
{196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145}, {236, 145},
{246, 141}, {252, 125}, {260, 129}, {280, 133},
};
const int num_vehicles = 1;
const RoutingIndexManager::NodeIndex depot{0};
};
Java
static class DataModel {
public final int[][] locations = {{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157},
{246, 157}, {236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169},
{196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145}, {156, 145},
{148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169}, {156, 169}, {140, 169},
{132, 169}, {124, 169}, {116, 161}, {104, 153}, {104, 161}, {104, 169}, {90, 165},
{80, 157}, {64, 157}, {64, 165}, {56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137},
{56, 129}, {56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153}, {40, 161},
{40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145}, {32, 137}, {32, 129}, {32, 121},
{32, 113}, {40, 113}, {56, 113}, {56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89},
{24, 89}, {16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81}, {8, 73}, {8, 65},
{8, 57}, {16, 57}, {8, 49}, {8, 41}, {24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65},
{32, 73}, {32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43}, {44, 35}, {44, 27},
{32, 25}, {24, 25}, {16, 25}, {16, 17}, {24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17},
{56, 25}, {56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49}, {48, 51}, {56, 57},
{56, 65}, {48, 63}, {48, 73}, {56, 73}, {56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97},
{104, 105}, {104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145},
{124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137}, {164, 137},
{172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93}, {172, 85}, {180, 85}, {180, 77},
{180, 69}, {180, 61}, {180, 53}, {172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81},
{148, 85}, {124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101}, {104, 89},
{104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41}, {104, 33}, {104, 25}, {104, 17},
{92, 9}, {80, 9}, {72, 9}, {64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49},
{104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61}, {124, 61}, {124, 53},
{124, 45}, {124, 37}, {124, 29}, {132, 21}, {124, 21}, {120, 9}, {128, 9}, {136, 9},
{148, 9}, {162, 9}, {156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37},
{172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57}, {212, 65}, {220, 73},
{228, 69}, {228, 77}, {236, 77}, {236, 69}, {236, 61}, {228, 61}, {228, 53}, {236, 53},
{236, 45}, {228, 45}, {228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21},
{252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61}, {260, 69}, {260, 77},
{276, 77}, {276, 69}, {276, 61}, {276, 53}, {284, 53}, {284, 61}, {284, 69}, {284, 77},
{284, 85}, {284, 93}, {284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85},
{268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85}, {228, 85}, {228, 93},
{236, 93}, {236, 101}, {228, 101}, {228, 109}, {228, 117}, {228, 125}, {220, 125},
{212, 117}, {204, 109}, {196, 101}, {188, 93}, {180, 93}, {180, 101}, {180, 109},
{180, 117}, {180, 125}, {196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145},
{236, 145}, {246, 141}, {252, 125}, {260, 129}, {280, 133}};
public final int vehicleNumber = 1;
public final int depot = 0;
}
C#
class DataModel
{
public int[,] Locations = {
{ 288, 149 }, { 288, 129 }, { 270, 133 }, { 256, 141 }, { 256, 157 }, { 246, 157 }, { 236, 169 },
{ 228, 169 }, { 228, 161 }, { 220, 169 }, { 212, 169 }, { 204, 169 }, { 196, 169 }, { 188, 169 },
{ 196, 161 }, { 188, 145 }, { 172, 145 }, { 164, 145 }, { 156, 145 }, { 148, 145 }, { 140, 145 },
{ 148, 169 }, { 164, 169 }, { 172, 169 }, { 156, 169 }, { 140, 169 }, { 132, 169 }, { 124, 169 },
{ 116, 161 }, { 104, 153 }, { 104, 161 }, { 104, 169 }, { 90, 165 }, { 80, 157 }, { 64, 157 },
{ 64, 165 }, { 56, 169 }, { 56, 161 }, { 56, 153 }, { 56, 145 }, { 56, 137 }, { 56, 129 },
{ 56, 121 }, { 40, 121 }, { 40, 129 }, { 40, 137 }, { 40, 145 }, { 40, 153 }, { 40, 161 },
{ 40, 169 }, { 32, 169 }, { 32, 161 }, { 32, 153 }, { 32, 145 }, { 32, 137 }, { 32, 129 },
{ 32, 121 }, { 32, 113 }, { 40, 113 }, { 56, 113 }, { 56, 105 }, { 48, 99 }, { 40, 99 },
{ 32, 97 }, { 32, 89 }, { 24, 89 }, { 16, 97 }, { 16, 109 }, { 8, 109 }, { 8, 97 },
{ 8, 89 }, { 8, 81 }, { 8, 73 }, { 8, 65 }, { 8, 57 }, { 16, 57 }, { 8, 49 },
{ 8, 41 }, { 24, 45 }, { 32, 41 }, { 32, 49 }, { 32, 57 }, { 32, 65 }, { 32, 73 },
{ 32, 81 }, { 40, 83 }, { 40, 73 }, { 40, 63 }, { 40, 51 }, { 44, 43 }, { 44, 35 },
{ 44, 27 }, { 32, 25 }, { 24, 25 }, { 16, 25 }, { 16, 17 }, { 24, 17 }, { 32, 17 },
{ 44, 11 }, { 56, 9 }, { 56, 17 }, { 56, 25 }, { 56, 33 }, { 56, 41 }, { 64, 41 },
{ 72, 41 }, { 72, 49 }, { 56, 49 }, { 48, 51 }, { 56, 57 }, { 56, 65 }, { 48, 63 },
{ 48, 73 }, { 56, 73 }, { 56, 81 }, { 48, 83 }, { 56, 89 }, { 56, 97 }, { 104, 97 },
{ 104, 105 }, { 104, 113 }, { 104, 121 }, { 104, 129 }, { 104, 137 }, { 104, 145 }, { 116, 145 },
{ 124, 145 }, { 132, 145 }, { 132, 137 }, { 140, 137 }, { 148, 137 }, { 156, 137 }, { 164, 137 },
{ 172, 125 }, { 172, 117 }, { 172, 109 }, { 172, 101 }, { 172, 93 }, { 172, 85 }, { 180, 85 },
{ 180, 77 }, { 180, 69 }, { 180, 61 }, { 180, 53 }, { 172, 53 }, { 172, 61 }, { 172, 69 },
{ 172, 77 }, { 164, 81 }, { 148, 85 }, { 124, 85 }, { 124, 93 }, { 124, 109 }, { 124, 125 },
{ 124, 117 }, { 124, 101 }, { 104, 89 }, { 104, 81 }, { 104, 73 }, { 104, 65 }, { 104, 49 },
{ 104, 41 }, { 104, 33 }, { 104, 25 }, { 104, 17 }, { 92, 9 }, { 80, 9 }, { 72, 9 },
{ 64, 21 }, { 72, 25 }, { 80, 25 }, { 80, 25 }, { 80, 41 }, { 88, 49 }, { 104, 57 },
{ 124, 69 }, { 124, 77 }, { 132, 81 }, { 140, 65 }, { 132, 61 }, { 124, 61 }, { 124, 53 },
{ 124, 45 }, { 124, 37 }, { 124, 29 }, { 132, 21 }, { 124, 21 }, { 120, 9 }, { 128, 9 },
{ 136, 9 }, { 148, 9 }, { 162, 9 }, { 156, 25 }, { 172, 21 }, { 180, 21 }, { 180, 29 },
{ 172, 29 }, { 172, 37 }, { 172, 45 }, { 180, 45 }, { 180, 37 }, { 188, 41 }, { 196, 49 },
{ 204, 57 }, { 212, 65 }, { 220, 73 }, { 228, 69 }, { 228, 77 }, { 236, 77 }, { 236, 69 },
{ 236, 61 }, { 228, 61 }, { 228, 53 }, { 236, 53 }, { 236, 45 }, { 228, 45 }, { 228, 37 },
{ 236, 37 }, { 236, 29 }, { 228, 29 }, { 228, 21 }, { 236, 21 }, { 252, 21 }, { 260, 29 },
{ 260, 37 }, { 260, 45 }, { 260, 53 }, { 260, 61 }, { 260, 69 }, { 260, 77 }, { 276, 77 },
{ 276, 69 }, { 276, 61 }, { 276, 53 }, { 284, 53 }, { 284, 61 }, { 284, 69 }, { 284, 77 },
{ 284, 85 }, { 284, 93 }, { 284, 101 }, { 288, 109 }, { 280, 109 }, { 276, 101 }, { 276, 93 },
{ 276, 85 }, { 268, 97 }, { 260, 109 }, { 252, 101 }, { 260, 93 }, { 260, 85 }, { 236, 85 },
{ 228, 85 }, { 228, 93 }, { 236, 93 }, { 236, 101 }, { 228, 101 }, { 228, 109 }, { 228, 117 },
{ 228, 125 }, { 220, 125 }, { 212, 117 }, { 204, 109 }, { 196, 101 }, { 188, 93 }, { 180, 93 },
{ 180, 101 }, { 180, 109 }, { 180, 117 }, { 180, 125 }, { 196, 145 }, { 204, 145 }, { 212, 145 },
{ 220, 145 }, { 228, 145 }, { 236, 145 }, { 246, 141 }, { 252, 125 }, { 260, 129 }, { 280, 133 },
};
public int VehicleNumber = 1;
public int Depot = 0;
};
Calcula la matriz de distancia
La siguiente función calcula la distancia euclidiana entre dos puntos en los datos y los almacena en un arreglo. Debido a que el solucionador de enrutamiento funciona sobre los números enteros, la función redondea las distancias computadas a números enteros. El redondeo no afecta la solución en este ejemplo, pero podría hacerlo en otros casos. Consulta Escala la matriz de distancia para evitar posibles problemas de redondeo.
Python
def compute_euclidean_distance_matrix(locations):
"""Creates callback to return distance between points."""
distances = {}
for from_counter, from_node in enumerate(locations):
distances[from_counter] = {}
for to_counter, to_node in enumerate(locations):
if from_counter == to_counter:
distances[from_counter][to_counter] = 0
else:
# Euclidean distance
distances[from_counter][to_counter] = int(
math.hypot((from_node[0] - to_node[0]), (from_node[1] - to_node[1]))
)
return distances
C++
// @brief Generate distance matrix.
std::vector<std::vector<int64_t>> ComputeEuclideanDistanceMatrix(
const std::vector<std::vector<int>>& locations) {
std::vector<std::vector<int64_t>> distances =
std::vector<std::vector<int64_t>>(
locations.size(), std::vector<int64_t>(locations.size(), int64_t{0}));
for (int from_node = 0; from_node < locations.size(); from_node++) {
for (int to_node = 0; to_node < locations.size(); to_node++) {
if (from_node != to_node)
distances[from_node][to_node] = static_cast<int64_t>(
std::hypot((locations[to_node][0] - locations[from_node][0]),
(locations[to_node][1] - locations[from_node][1])));
}
}
return distances;
}
Java
/// @brief Compute Euclidean distance matrix from locations array.
/// @details It uses an array of locations and computes
/// the Euclidean distance between any two locations.
private static long[][] computeEuclideanDistanceMatrix(int[][] locations) {
// Calculate distance matrix using Euclidean distance.
long[][] distanceMatrix = new long[locations.length][locations.length];
for (int fromNode = 0; fromNode < locations.length; ++fromNode) {
for (int toNode = 0; toNode < locations.length; ++toNode) {
if (fromNode == toNode) {
distanceMatrix[fromNode][toNode] = 0;
} else {
distanceMatrix[fromNode][toNode] =
(long) Math.hypot(locations[toNode][0] - locations[fromNode][0],
locations[toNode][1] - locations[fromNode][1]);
}
}
}
return distanceMatrix;
}
C#
/// <summary>
/// Euclidean distance implemented as a callback. It uses an array of
/// positions and computes the Euclidean distance between the two
/// positions of two different indices.
/// </summary>
static long[,] ComputeEuclideanDistanceMatrix(in int[,] locations)
{
// Calculate the distance matrix using Euclidean distance.
int locationNumber = locations.GetLength(0);
long[,] distanceMatrix = new long[locationNumber, locationNumber];
for (int fromNode = 0; fromNode < locationNumber; fromNode++)
{
for (int toNode = 0; toNode < locationNumber; toNode++)
{
if (fromNode == toNode)
distanceMatrix[fromNode, toNode] = 0;
else
distanceMatrix[fromNode, toNode] =
(long)Math.Sqrt(Math.Pow(locations[toNode, 0] - locations[fromNode, 0], 2) +
Math.Pow(locations[toNode, 1] - locations[fromNode, 1], 2));
}
}
return distanceMatrix;
}
Cómo agregar la devolución de llamada de distancia
El código que crea la devolución de llamada de distancia es casi el mismo que en el ejemplo anterior. Sin embargo, en este caso, el programa llama a la función que calcula la matriz de distancia antes de agregar la devolución de llamada.
Python
distance_matrix = compute_euclidean_distance_matrix(data["locations"])
def distance_callback(from_index, to_index):
"""Returns the distance between the two nodes."""
# Convert from routing variable Index to distance matrix NodeIndex.
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return distance_matrix[from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
C++
const auto distance_matrix = ComputeEuclideanDistanceMatrix(data.locations);
const int transit_callback_index = routing.RegisterTransitCallback(
[&distance_matrix, &manager](const int64_t from_index,
const int64_t to_index) -> int64_t {
// Convert from routing variable Index to distance matrix NodeIndex.
const int from_node = manager.IndexToNode(from_index).value();
const int to_node = manager.IndexToNode(to_index).value();
return distance_matrix[from_node][to_node];
});
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
Java
final long[][] distanceMatrix = computeEuclideanDistanceMatrix(data.locations);
final int transitCallbackIndex =
routing.registerTransitCallback((long fromIndex, long toIndex) -> {
// Convert from routing variable Index to user NodeIndex.
int fromNode = manager.indexToNode(fromIndex);
int toNode = manager.indexToNode(toIndex);
return distanceMatrix[fromNode][toNode];
});
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
C#
long[,] distanceMatrix = ComputeEuclideanDistanceMatrix(data.Locations);
int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
{
// Convert from routing variable Index to
// distance matrix NodeIndex.
var fromNode = manager.IndexToNode(fromIndex);
var toNode = manager.IndexToNode(toIndex);
return distanceMatrix[fromNode, toNode];
});
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
Impresora de soluciones
La siguiente función imprime la solución en la consola. Para mantener un resultado más compacto, la función muestra solo los índices de las ubicaciones en la ruta.
Python
def print_solution(manager, routing, solution):
"""Prints solution on console."""
print(f"Objective: {solution.ObjectiveValue()}")
index = routing.Start(0)
plan_output = "Route:\n"
route_distance = 0
while not routing.IsEnd(index):
plan_output += f" {manager.IndexToNode(index)} ->"
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(previous_index, index, 0)
plan_output += f" {manager.IndexToNode(index)}\n"
print(plan_output)
plan_output += f"Objective: {route_distance}m\n"
C++
//! @brief Print the solution
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const RoutingIndexManager& manager,
const RoutingModel& routing, const Assignment& solution) {
LOG(INFO) << "Objective: " << solution.ObjectiveValue();
// Inspect solution.
int64_t index = routing.Start(0);
LOG(INFO) << "Route:";
int64_t distance{0};
std::stringstream route;
while (!routing.IsEnd(index)) {
route << manager.IndexToNode(index).value() << " -> ";
const int64_t previous_index = index;
index = solution.Value(routing.NextVar(index));
distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0});
}
LOG(INFO) << route.str() << manager.IndexToNode(index).value();
LOG(INFO) << "Route distance: " << distance << "miles";
LOG(INFO) << "";
LOG(INFO) << "Advanced usage:";
LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}
Java
/// @brief Print the solution.
static void printSolution(
RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
// Solution cost.
logger.info("Objective: " + solution.objectiveValue());
// Inspect solution.
logger.info("Route:");
long routeDistance = 0;
String route = "";
long index = routing.start(0);
while (!routing.isEnd(index)) {
route += manager.indexToNode(index) + " -> ";
long previousIndex = index;
index = solution.value(routing.nextVar(index));
routing.getArcCostForVehicle(previousIndex, index, 0);
}
route += manager.indexToNode(routing.end(0));
logger.info(route);
logger.info("Route distance: " + routeDistance);
}
C#
/// <summary>
/// Print the solution.
/// </summary>
static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution)
{
Console.WriteLine("Objective: {0}", solution.ObjectiveValue());
// Inspect solution.
Console.WriteLine("Route:");
long routeDistance = 0;
var index = routing.Start(0);
while (routing.IsEnd(index) == false)
{
Console.Write("{0} -> ", manager.IndexToNode((int)index));
var previousIndex = index;
index = solution.Value(routing.NextVar(index));
routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0);
}
Console.WriteLine("{0}", manager.IndexToNode((int)index));
Console.WriteLine("Route distance: {0}m", routeDistance);
}
Función principal
La función principal es básicamente la misma que la del ejemplo anterior, pero también incluye una llamada a la función que crea la matriz de distancia.
Cómo ejecutar el programa
Los programas completos se muestran en la siguiente sección. Cuando ejecutas el programa, se muestra la siguiente ruta:
Total distance: 2790 Route of vehicle 0: 0 -> 1 -> 279 -> 2 -> 278 -> 277 -> 247 -> 248 -> 249 -> 246 -> 244 -> 243 -> 242 -> 241 -> 240 -> 239 -> 238 -> 237 -> 236 -> 235 -> 234 -> 233 -> 232 -> 231 -> 230 -> 245 -> 250 -> 229 -> 228 -> 227 -> 226 -> 225 -> 224 -> 223 -> 222 -> 221 -> 220 -> 219 -> 218 -> 217 -> 216 -> 215 -> 214 -> 213 -> 212 -> 211 -> 210 -> 209 -> 208 -> 251 -> 254 -> 255 -> 257 -> 256 -> 253 -> 252 -> 207 -> 206 -> 205 -> 204 -> 203 -> 202 -> 142 -> 141 -> 146 -> 147 -> 140 -> 139 -> 265 -> 136 -> 137 -> 138 -> 148 -> 149 -> 177 -> 176 -> 175 -> 178 -> 179 -> 180 -> 181 -> 182 -> 183 -> 184 -> 186 -> 185 -> 192 -> 196 -> 197 -> 198 -> 144 -> 145 -> 143 -> 199 -> 201 -> 200 -> 195 -> 194 -> 193 -> 191 -> 190 -> 189 -> 188 -> 187 -> 163 -> 164 -> 165 -> 166 -> 167 -> 168 -> 169 -> 171 -> 170 -> 172 -> 105 -> 106 -> 104 -> 103 -> 107 -> 109 -> 110 -> 113 -> 114 -> 116 -> 117 -> 61 -> 62 -> 63 -> 65 -> 64 -> 84 -> 85 -> 115 -> 112 -> 86 -> 83 -> 82 -> 87 -> 111 -> 108 -> 89 -> 90 -> 91 -> 102 -> 101 -> 100 -> 99 -> 98 -> 97 -> 96 -> 95 -> 94 -> 93 -> 92 -> 79 -> 88 -> 81 -> 80 -> 78 -> 77 -> 76 -> 74 -> 75 -> 73 -> 72 -> 71 -> 70 -> 69 -> 66 -> 68 -> 67 -> 57 -> 56 -> 55 -> 54 -> 53 -> 52 -> 51 -> 50 -> 49 -> 48 -> 47 -> 46 -> 45 -> 44 -> 43 -> 58 -> 60 -> 59 -> 42 -> 41 -> 40 -> 39 -> 38 -> 37 -> 36 -> 35 -> 34 -> 33 -> 32 -> 31 -> 30 -> 29 -> 124 -> 123 -> 122 -> 121 -> 120 -> 119 -> 118 -> 156 -> 157 -> 158 -> 173 -> 162 -> 161 -> 160 -> 174 -> 159 -> 150 -> 151 -> 155 -> 152 -> 154 -> 153 -> 128 -> 129 -> 130 -> 131 -> 18 -> 19 -> 20 -> 127 -> 126 -> 125 -> 28 -> 27 -> 26 -> 25 -> 21 -> 24 -> 22 -> 23 -> 13 -> 12 -> 14 -> 11 -> 10 -> 9 -> 7 -> 8 -> 6 -> 5 -> 275 -> 274 -> 273 -> 272 -> 271 -> 270 -> 15 -> 16 -> 17 -> 132 -> 133 -> 269 -> 268 -> 134 -> 135 -> 267 -> 266 -> 264 -> 263 -> 262 -> 261 -> 260 -> 258 -> 259 -> 276 -> 3 -> 4 -> 0
Este es el gráfico de la ruta correspondiente:
La biblioteca de herramientas OR encuentra la visita anterior con mucha rapidez: en menos de un segundo en una computadora típica. La duración total del recorrido anterior es de 2,790.
Programas completos
Estos son los programas completos para el ejemplo de la placa de circuito.
Python
"""Simple Travelling Salesperson Problem (TSP) on a circuit board."""
import math
from ortools.constraint_solver import routing_enums_pb2
from ortools.constraint_solver import pywrapcp
def create_data_model():
"""Stores the data for the problem."""
data = {}
# Locations in block units
data["locations"] = [
# fmt: off
(288, 149), (288, 129), (270, 133), (256, 141), (256, 157), (246, 157),
(236, 169), (228, 169), (228, 161), (220, 169), (212, 169), (204, 169),
(196, 169), (188, 169), (196, 161), (188, 145), (172, 145), (164, 145),
(156, 145), (148, 145), (140, 145), (148, 169), (164, 169), (172, 169),
(156, 169), (140, 169), (132, 169), (124, 169), (116, 161), (104, 153),
(104, 161), (104, 169), (90, 165), (80, 157), (64, 157), (64, 165),
(56, 169), (56, 161), (56, 153), (56, 145), (56, 137), (56, 129),
(56, 121), (40, 121), (40, 129), (40, 137), (40, 145), (40, 153),
(40, 161), (40, 169), (32, 169), (32, 161), (32, 153), (32, 145),
(32, 137), (32, 129), (32, 121), (32, 113), (40, 113), (56, 113),
(56, 105), (48, 99), (40, 99), (32, 97), (32, 89), (24, 89),
(16, 97), (16, 109), (8, 109), (8, 97), (8, 89), (8, 81),
(8, 73), (8, 65), (8, 57), (16, 57), (8, 49), (8, 41),
(24, 45), (32, 41), (32, 49), (32, 57), (32, 65), (32, 73),
(32, 81), (40, 83), (40, 73), (40, 63), (40, 51), (44, 43),
(44, 35), (44, 27), (32, 25), (24, 25), (16, 25), (16, 17),
(24, 17), (32, 17), (44, 11), (56, 9), (56, 17), (56, 25),
(56, 33), (56, 41), (64, 41), (72, 41), (72, 49), (56, 49),
(48, 51), (56, 57), (56, 65), (48, 63), (48, 73), (56, 73),
(56, 81), (48, 83), (56, 89), (56, 97), (104, 97), (104, 105),
(104, 113), (104, 121), (104, 129), (104, 137), (104, 145), (116, 145),
(124, 145), (132, 145), (132, 137), (140, 137), (148, 137), (156, 137),
(164, 137), (172, 125), (172, 117), (172, 109), (172, 101), (172, 93),
(172, 85), (180, 85), (180, 77), (180, 69), (180, 61), (180, 53),
(172, 53), (172, 61), (172, 69), (172, 77), (164, 81), (148, 85),
(124, 85), (124, 93), (124, 109), (124, 125), (124, 117), (124, 101),
(104, 89), (104, 81), (104, 73), (104, 65), (104, 49), (104, 41),
(104, 33), (104, 25), (104, 17), (92, 9), (80, 9), (72, 9),
(64, 21), (72, 25), (80, 25), (80, 25), (80, 41), (88, 49),
(104, 57), (124, 69), (124, 77), (132, 81), (140, 65), (132, 61),
(124, 61), (124, 53), (124, 45), (124, 37), (124, 29), (132, 21),
(124, 21), (120, 9), (128, 9), (136, 9), (148, 9), (162, 9),
(156, 25), (172, 21), (180, 21), (180, 29), (172, 29), (172, 37),
(172, 45), (180, 45), (180, 37), (188, 41), (196, 49), (204, 57),
(212, 65), (220, 73), (228, 69), (228, 77), (236, 77), (236, 69),
(236, 61), (228, 61), (228, 53), (236, 53), (236, 45), (228, 45),
(228, 37), (236, 37), (236, 29), (228, 29), (228, 21), (236, 21),
(252, 21), (260, 29), (260, 37), (260, 45), (260, 53), (260, 61),
(260, 69), (260, 77), (276, 77), (276, 69), (276, 61), (276, 53),
(284, 53), (284, 61), (284, 69), (284, 77), (284, 85), (284, 93),
(284, 101), (288, 109), (280, 109), (276, 101), (276, 93), (276, 85),
(268, 97), (260, 109), (252, 101), (260, 93), (260, 85), (236, 85),
(228, 85), (228, 93), (236, 93), (236, 101), (228, 101), (228, 109),
(228, 117), (228, 125), (220, 125), (212, 117), (204, 109), (196, 101),
(188, 93), (180, 93), (180, 101), (180, 109), (180, 117), (180, 125),
(196, 145), (204, 145), (212, 145), (220, 145), (228, 145), (236, 145),
(246, 141), (252, 125), (260, 129), (280, 133)
# fmt: on
]
data["num_vehicles"] = 1
data["depot"] = 0
return data
def compute_euclidean_distance_matrix(locations):
"""Creates callback to return distance between points."""
distances = {}
for from_counter, from_node in enumerate(locations):
distances[from_counter] = {}
for to_counter, to_node in enumerate(locations):
if from_counter == to_counter:
distances[from_counter][to_counter] = 0
else:
# Euclidean distance
distances[from_counter][to_counter] = int(
math.hypot((from_node[0] - to_node[0]), (from_node[1] - to_node[1]))
)
return distances
def print_solution(manager, routing, solution):
"""Prints solution on console."""
print(f"Objective: {solution.ObjectiveValue()}")
index = routing.Start(0)
plan_output = "Route:\n"
route_distance = 0
while not routing.IsEnd(index):
plan_output += f" {manager.IndexToNode(index)} ->"
previous_index = index
index = solution.Value(routing.NextVar(index))
route_distance += routing.GetArcCostForVehicle(previous_index, index, 0)
plan_output += f" {manager.IndexToNode(index)}\n"
print(plan_output)
plan_output += f"Objective: {route_distance}m\n"
def main():
"""Entry point of the program."""
# Instantiate the data problem.
data = create_data_model()
# Create the routing index manager.
manager = pywrapcp.RoutingIndexManager(
len(data["locations"]), data["num_vehicles"], data["depot"]
)
# Create Routing Model.
routing = pywrapcp.RoutingModel(manager)
distance_matrix = compute_euclidean_distance_matrix(data["locations"])
def distance_callback(from_index, to_index):
"""Returns the distance between the two nodes."""
# Convert from routing variable Index to distance matrix NodeIndex.
from_node = manager.IndexToNode(from_index)
to_node = manager.IndexToNode(to_index)
return distance_matrix[from_node][to_node]
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
# Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
# Setting first solution heuristic.
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.first_solution_strategy = (
routing_enums_pb2.FirstSolutionStrategy.PATH_CHEAPEST_ARC
)
# Solve the problem.
solution = routing.SolveWithParameters(search_parameters)
# Print solution on console.
if solution:
print_solution(manager, routing, solution)
if __name__ == "__main__":
main()
C++
#include <cmath>
#include <cstdint>
#include <sstream>
#include <vector>
#include "ortools/constraint_solver/routing.h"
#include "ortools/constraint_solver/routing_enums.pb.h"
#include "ortools/constraint_solver/routing_index_manager.h"
#include "ortools/constraint_solver/routing_parameters.h"
namespace operations_research {
struct DataModel {
const std::vector<std::vector<int>> locations{
{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157}, {246, 157},
{236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169},
{196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145},
{156, 145}, {148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169},
{156, 169}, {140, 169}, {132, 169}, {124, 169}, {116, 161}, {104, 153},
{104, 161}, {104, 169}, {90, 165}, {80, 157}, {64, 157}, {64, 165},
{56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137}, {56, 129},
{56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153},
{40, 161}, {40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145},
{32, 137}, {32, 129}, {32, 121}, {32, 113}, {40, 113}, {56, 113},
{56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89}, {24, 89},
{16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81},
{8, 73}, {8, 65}, {8, 57}, {16, 57}, {8, 49}, {8, 41},
{24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65}, {32, 73},
{32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43},
{44, 35}, {44, 27}, {32, 25}, {24, 25}, {16, 25}, {16, 17},
{24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17}, {56, 25},
{56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49},
{48, 51}, {56, 57}, {56, 65}, {48, 63}, {48, 73}, {56, 73},
{56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97}, {104, 105},
{104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145},
{124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137},
{164, 137}, {172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93},
{172, 85}, {180, 85}, {180, 77}, {180, 69}, {180, 61}, {180, 53},
{172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81}, {148, 85},
{124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101},
{104, 89}, {104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41},
{104, 33}, {104, 25}, {104, 17}, {92, 9}, {80, 9}, {72, 9},
{64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49},
{104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61},
{124, 61}, {124, 53}, {124, 45}, {124, 37}, {124, 29}, {132, 21},
{124, 21}, {120, 9}, {128, 9}, {136, 9}, {148, 9}, {162, 9},
{156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37},
{172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57},
{212, 65}, {220, 73}, {228, 69}, {228, 77}, {236, 77}, {236, 69},
{236, 61}, {228, 61}, {228, 53}, {236, 53}, {236, 45}, {228, 45},
{228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21},
{252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61},
{260, 69}, {260, 77}, {276, 77}, {276, 69}, {276, 61}, {276, 53},
{284, 53}, {284, 61}, {284, 69}, {284, 77}, {284, 85}, {284, 93},
{284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85},
{268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85},
{228, 85}, {228, 93}, {236, 93}, {236, 101}, {228, 101}, {228, 109},
{228, 117}, {228, 125}, {220, 125}, {212, 117}, {204, 109}, {196, 101},
{188, 93}, {180, 93}, {180, 101}, {180, 109}, {180, 117}, {180, 125},
{196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145}, {236, 145},
{246, 141}, {252, 125}, {260, 129}, {280, 133},
};
const int num_vehicles = 1;
const RoutingIndexManager::NodeIndex depot{0};
};
// @brief Generate distance matrix.
std::vector<std::vector<int64_t>> ComputeEuclideanDistanceMatrix(
const std::vector<std::vector<int>>& locations) {
std::vector<std::vector<int64_t>> distances =
std::vector<std::vector<int64_t>>(
locations.size(), std::vector<int64_t>(locations.size(), int64_t{0}));
for (int from_node = 0; from_node < locations.size(); from_node++) {
for (int to_node = 0; to_node < locations.size(); to_node++) {
if (from_node != to_node)
distances[from_node][to_node] = static_cast<int64_t>(
std::hypot((locations[to_node][0] - locations[from_node][0]),
(locations[to_node][1] - locations[from_node][1])));
}
}
return distances;
}
//! @brief Print the solution
//! @param[in] manager Index manager used.
//! @param[in] routing Routing solver used.
//! @param[in] solution Solution found by the solver.
void PrintSolution(const RoutingIndexManager& manager,
const RoutingModel& routing, const Assignment& solution) {
LOG(INFO) << "Objective: " << solution.ObjectiveValue();
// Inspect solution.
int64_t index = routing.Start(0);
LOG(INFO) << "Route:";
int64_t distance{0};
std::stringstream route;
while (!routing.IsEnd(index)) {
route << manager.IndexToNode(index).value() << " -> ";
const int64_t previous_index = index;
index = solution.Value(routing.NextVar(index));
distance += routing.GetArcCostForVehicle(previous_index, index, int64_t{0});
}
LOG(INFO) << route.str() << manager.IndexToNode(index).value();
LOG(INFO) << "Route distance: " << distance << "miles";
LOG(INFO) << "";
LOG(INFO) << "Advanced usage:";
LOG(INFO) << "Problem solved in " << routing.solver()->wall_time() << "ms";
}
void Tsp() {
// Instantiate the data problem.
DataModel data;
// Create Routing Index Manager
RoutingIndexManager manager(data.locations.size(), data.num_vehicles,
data.depot);
// Create Routing Model.
RoutingModel routing(manager);
const auto distance_matrix = ComputeEuclideanDistanceMatrix(data.locations);
const int transit_callback_index = routing.RegisterTransitCallback(
[&distance_matrix, &manager](const int64_t from_index,
const int64_t to_index) -> int64_t {
// Convert from routing variable Index to distance matrix NodeIndex.
const int from_node = manager.IndexToNode(from_index).value();
const int to_node = manager.IndexToNode(to_index).value();
return distance_matrix[from_node][to_node];
});
// Define cost of each arc.
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
searchParameters.set_first_solution_strategy(
FirstSolutionStrategy::PATH_CHEAPEST_ARC);
// Solve the problem.
const Assignment* solution = routing.SolveWithParameters(searchParameters);
// Print solution on console.
PrintSolution(manager, routing, *solution);
}
} // namespace operations_research
int main(int /*argc*/, char* /*argv*/[]) {
operations_research::Tsp();
return EXIT_SUCCESS;
}
Java
package com.google.ortools.constraintsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.Assignment;
import com.google.ortools.constraintsolver.FirstSolutionStrategy;
import com.google.ortools.constraintsolver.RoutingIndexManager;
import com.google.ortools.constraintsolver.RoutingModel;
import com.google.ortools.constraintsolver.RoutingSearchParameters;
import com.google.ortools.constraintsolver.main;
import java.util.logging.Logger;
/** Minimal TSP. */
public class TspCircuitBoard {
private static final Logger logger = Logger.getLogger(TspCircuitBoard.class.getName());
static class DataModel {
public final int[][] locations = {{288, 149}, {288, 129}, {270, 133}, {256, 141}, {256, 157},
{246, 157}, {236, 169}, {228, 169}, {228, 161}, {220, 169}, {212, 169}, {204, 169},
{196, 169}, {188, 169}, {196, 161}, {188, 145}, {172, 145}, {164, 145}, {156, 145},
{148, 145}, {140, 145}, {148, 169}, {164, 169}, {172, 169}, {156, 169}, {140, 169},
{132, 169}, {124, 169}, {116, 161}, {104, 153}, {104, 161}, {104, 169}, {90, 165},
{80, 157}, {64, 157}, {64, 165}, {56, 169}, {56, 161}, {56, 153}, {56, 145}, {56, 137},
{56, 129}, {56, 121}, {40, 121}, {40, 129}, {40, 137}, {40, 145}, {40, 153}, {40, 161},
{40, 169}, {32, 169}, {32, 161}, {32, 153}, {32, 145}, {32, 137}, {32, 129}, {32, 121},
{32, 113}, {40, 113}, {56, 113}, {56, 105}, {48, 99}, {40, 99}, {32, 97}, {32, 89},
{24, 89}, {16, 97}, {16, 109}, {8, 109}, {8, 97}, {8, 89}, {8, 81}, {8, 73}, {8, 65},
{8, 57}, {16, 57}, {8, 49}, {8, 41}, {24, 45}, {32, 41}, {32, 49}, {32, 57}, {32, 65},
{32, 73}, {32, 81}, {40, 83}, {40, 73}, {40, 63}, {40, 51}, {44, 43}, {44, 35}, {44, 27},
{32, 25}, {24, 25}, {16, 25}, {16, 17}, {24, 17}, {32, 17}, {44, 11}, {56, 9}, {56, 17},
{56, 25}, {56, 33}, {56, 41}, {64, 41}, {72, 41}, {72, 49}, {56, 49}, {48, 51}, {56, 57},
{56, 65}, {48, 63}, {48, 73}, {56, 73}, {56, 81}, {48, 83}, {56, 89}, {56, 97}, {104, 97},
{104, 105}, {104, 113}, {104, 121}, {104, 129}, {104, 137}, {104, 145}, {116, 145},
{124, 145}, {132, 145}, {132, 137}, {140, 137}, {148, 137}, {156, 137}, {164, 137},
{172, 125}, {172, 117}, {172, 109}, {172, 101}, {172, 93}, {172, 85}, {180, 85}, {180, 77},
{180, 69}, {180, 61}, {180, 53}, {172, 53}, {172, 61}, {172, 69}, {172, 77}, {164, 81},
{148, 85}, {124, 85}, {124, 93}, {124, 109}, {124, 125}, {124, 117}, {124, 101}, {104, 89},
{104, 81}, {104, 73}, {104, 65}, {104, 49}, {104, 41}, {104, 33}, {104, 25}, {104, 17},
{92, 9}, {80, 9}, {72, 9}, {64, 21}, {72, 25}, {80, 25}, {80, 25}, {80, 41}, {88, 49},
{104, 57}, {124, 69}, {124, 77}, {132, 81}, {140, 65}, {132, 61}, {124, 61}, {124, 53},
{124, 45}, {124, 37}, {124, 29}, {132, 21}, {124, 21}, {120, 9}, {128, 9}, {136, 9},
{148, 9}, {162, 9}, {156, 25}, {172, 21}, {180, 21}, {180, 29}, {172, 29}, {172, 37},
{172, 45}, {180, 45}, {180, 37}, {188, 41}, {196, 49}, {204, 57}, {212, 65}, {220, 73},
{228, 69}, {228, 77}, {236, 77}, {236, 69}, {236, 61}, {228, 61}, {228, 53}, {236, 53},
{236, 45}, {228, 45}, {228, 37}, {236, 37}, {236, 29}, {228, 29}, {228, 21}, {236, 21},
{252, 21}, {260, 29}, {260, 37}, {260, 45}, {260, 53}, {260, 61}, {260, 69}, {260, 77},
{276, 77}, {276, 69}, {276, 61}, {276, 53}, {284, 53}, {284, 61}, {284, 69}, {284, 77},
{284, 85}, {284, 93}, {284, 101}, {288, 109}, {280, 109}, {276, 101}, {276, 93}, {276, 85},
{268, 97}, {260, 109}, {252, 101}, {260, 93}, {260, 85}, {236, 85}, {228, 85}, {228, 93},
{236, 93}, {236, 101}, {228, 101}, {228, 109}, {228, 117}, {228, 125}, {220, 125},
{212, 117}, {204, 109}, {196, 101}, {188, 93}, {180, 93}, {180, 101}, {180, 109},
{180, 117}, {180, 125}, {196, 145}, {204, 145}, {212, 145}, {220, 145}, {228, 145},
{236, 145}, {246, 141}, {252, 125}, {260, 129}, {280, 133}};
public final int vehicleNumber = 1;
public final int depot = 0;
}
/// @brief Compute Euclidean distance matrix from locations array.
/// @details It uses an array of locations and computes
/// the Euclidean distance between any two locations.
private static long[][] computeEuclideanDistanceMatrix(int[][] locations) {
// Calculate distance matrix using Euclidean distance.
long[][] distanceMatrix = new long[locations.length][locations.length];
for (int fromNode = 0; fromNode < locations.length; ++fromNode) {
for (int toNode = 0; toNode < locations.length; ++toNode) {
if (fromNode == toNode) {
distanceMatrix[fromNode][toNode] = 0;
} else {
distanceMatrix[fromNode][toNode] =
(long) Math.hypot(locations[toNode][0] - locations[fromNode][0],
locations[toNode][1] - locations[fromNode][1]);
}
}
}
return distanceMatrix;
}
/// @brief Print the solution.
static void printSolution(
RoutingModel routing, RoutingIndexManager manager, Assignment solution) {
// Solution cost.
logger.info("Objective: " + solution.objectiveValue());
// Inspect solution.
logger.info("Route:");
long routeDistance = 0;
String route = "";
long index = routing.start(0);
while (!routing.isEnd(index)) {
route += manager.indexToNode(index) + " -> ";
long previousIndex = index;
index = solution.value(routing.nextVar(index));
routing.getArcCostForVehicle(previousIndex, index, 0);
}
route += manager.indexToNode(routing.end(0));
logger.info(route);
logger.info("Route distance: " + routeDistance);
}
public static void main(String[] args) throws Exception {
Loader.loadNativeLibraries();
// Instantiate the data problem.
final DataModel data = new DataModel();
// Create Routing Index Manager
RoutingIndexManager manager =
new RoutingIndexManager(data.locations.length, data.vehicleNumber, data.depot);
// Create Routing Model.
RoutingModel routing = new RoutingModel(manager);
// Create and register a transit callback.
final long[][] distanceMatrix = computeEuclideanDistanceMatrix(data.locations);
final int transitCallbackIndex =
routing.registerTransitCallback((long fromIndex, long toIndex) -> {
// Convert from routing variable Index to user NodeIndex.
int fromNode = manager.indexToNode(fromIndex);
int toNode = manager.indexToNode(toIndex);
return distanceMatrix[fromNode][toNode];
});
// Define cost of each arc.
routing.setArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters =
main.defaultRoutingSearchParameters()
.toBuilder()
.setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
.build();
// Solve the problem.
Assignment solution = routing.solveWithParameters(searchParameters);
// Print solution on console.
printSolution(routing, manager, solution);
}
}
C#
using System;
using System.Collections.Generic;
using Google.OrTools.ConstraintSolver;
/// <summary>
/// Minimal TSP.
/// A description of the problem can be found here:
/// http://en.wikipedia.org/wiki/Travelling_salesperson_problem.
/// </summary>
public class TspCircuitBoard
{
class DataModel
{
public int[,] Locations = {
{ 288, 149 }, { 288, 129 }, { 270, 133 }, { 256, 141 }, { 256, 157 }, { 246, 157 }, { 236, 169 },
{ 228, 169 }, { 228, 161 }, { 220, 169 }, { 212, 169 }, { 204, 169 }, { 196, 169 }, { 188, 169 },
{ 196, 161 }, { 188, 145 }, { 172, 145 }, { 164, 145 }, { 156, 145 }, { 148, 145 }, { 140, 145 },
{ 148, 169 }, { 164, 169 }, { 172, 169 }, { 156, 169 }, { 140, 169 }, { 132, 169 }, { 124, 169 },
{ 116, 161 }, { 104, 153 }, { 104, 161 }, { 104, 169 }, { 90, 165 }, { 80, 157 }, { 64, 157 },
{ 64, 165 }, { 56, 169 }, { 56, 161 }, { 56, 153 }, { 56, 145 }, { 56, 137 }, { 56, 129 },
{ 56, 121 }, { 40, 121 }, { 40, 129 }, { 40, 137 }, { 40, 145 }, { 40, 153 }, { 40, 161 },
{ 40, 169 }, { 32, 169 }, { 32, 161 }, { 32, 153 }, { 32, 145 }, { 32, 137 }, { 32, 129 },
{ 32, 121 }, { 32, 113 }, { 40, 113 }, { 56, 113 }, { 56, 105 }, { 48, 99 }, { 40, 99 },
{ 32, 97 }, { 32, 89 }, { 24, 89 }, { 16, 97 }, { 16, 109 }, { 8, 109 }, { 8, 97 },
{ 8, 89 }, { 8, 81 }, { 8, 73 }, { 8, 65 }, { 8, 57 }, { 16, 57 }, { 8, 49 },
{ 8, 41 }, { 24, 45 }, { 32, 41 }, { 32, 49 }, { 32, 57 }, { 32, 65 }, { 32, 73 },
{ 32, 81 }, { 40, 83 }, { 40, 73 }, { 40, 63 }, { 40, 51 }, { 44, 43 }, { 44, 35 },
{ 44, 27 }, { 32, 25 }, { 24, 25 }, { 16, 25 }, { 16, 17 }, { 24, 17 }, { 32, 17 },
{ 44, 11 }, { 56, 9 }, { 56, 17 }, { 56, 25 }, { 56, 33 }, { 56, 41 }, { 64, 41 },
{ 72, 41 }, { 72, 49 }, { 56, 49 }, { 48, 51 }, { 56, 57 }, { 56, 65 }, { 48, 63 },
{ 48, 73 }, { 56, 73 }, { 56, 81 }, { 48, 83 }, { 56, 89 }, { 56, 97 }, { 104, 97 },
{ 104, 105 }, { 104, 113 }, { 104, 121 }, { 104, 129 }, { 104, 137 }, { 104, 145 }, { 116, 145 },
{ 124, 145 }, { 132, 145 }, { 132, 137 }, { 140, 137 }, { 148, 137 }, { 156, 137 }, { 164, 137 },
{ 172, 125 }, { 172, 117 }, { 172, 109 }, { 172, 101 }, { 172, 93 }, { 172, 85 }, { 180, 85 },
{ 180, 77 }, { 180, 69 }, { 180, 61 }, { 180, 53 }, { 172, 53 }, { 172, 61 }, { 172, 69 },
{ 172, 77 }, { 164, 81 }, { 148, 85 }, { 124, 85 }, { 124, 93 }, { 124, 109 }, { 124, 125 },
{ 124, 117 }, { 124, 101 }, { 104, 89 }, { 104, 81 }, { 104, 73 }, { 104, 65 }, { 104, 49 },
{ 104, 41 }, { 104, 33 }, { 104, 25 }, { 104, 17 }, { 92, 9 }, { 80, 9 }, { 72, 9 },
{ 64, 21 }, { 72, 25 }, { 80, 25 }, { 80, 25 }, { 80, 41 }, { 88, 49 }, { 104, 57 },
{ 124, 69 }, { 124, 77 }, { 132, 81 }, { 140, 65 }, { 132, 61 }, { 124, 61 }, { 124, 53 },
{ 124, 45 }, { 124, 37 }, { 124, 29 }, { 132, 21 }, { 124, 21 }, { 120, 9 }, { 128, 9 },
{ 136, 9 }, { 148, 9 }, { 162, 9 }, { 156, 25 }, { 172, 21 }, { 180, 21 }, { 180, 29 },
{ 172, 29 }, { 172, 37 }, { 172, 45 }, { 180, 45 }, { 180, 37 }, { 188, 41 }, { 196, 49 },
{ 204, 57 }, { 212, 65 }, { 220, 73 }, { 228, 69 }, { 228, 77 }, { 236, 77 }, { 236, 69 },
{ 236, 61 }, { 228, 61 }, { 228, 53 }, { 236, 53 }, { 236, 45 }, { 228, 45 }, { 228, 37 },
{ 236, 37 }, { 236, 29 }, { 228, 29 }, { 228, 21 }, { 236, 21 }, { 252, 21 }, { 260, 29 },
{ 260, 37 }, { 260, 45 }, { 260, 53 }, { 260, 61 }, { 260, 69 }, { 260, 77 }, { 276, 77 },
{ 276, 69 }, { 276, 61 }, { 276, 53 }, { 284, 53 }, { 284, 61 }, { 284, 69 }, { 284, 77 },
{ 284, 85 }, { 284, 93 }, { 284, 101 }, { 288, 109 }, { 280, 109 }, { 276, 101 }, { 276, 93 },
{ 276, 85 }, { 268, 97 }, { 260, 109 }, { 252, 101 }, { 260, 93 }, { 260, 85 }, { 236, 85 },
{ 228, 85 }, { 228, 93 }, { 236, 93 }, { 236, 101 }, { 228, 101 }, { 228, 109 }, { 228, 117 },
{ 228, 125 }, { 220, 125 }, { 212, 117 }, { 204, 109 }, { 196, 101 }, { 188, 93 }, { 180, 93 },
{ 180, 101 }, { 180, 109 }, { 180, 117 }, { 180, 125 }, { 196, 145 }, { 204, 145 }, { 212, 145 },
{ 220, 145 }, { 228, 145 }, { 236, 145 }, { 246, 141 }, { 252, 125 }, { 260, 129 }, { 280, 133 },
};
public int VehicleNumber = 1;
public int Depot = 0;
};
/// <summary>
/// Euclidean distance implemented as a callback. It uses an array of
/// positions and computes the Euclidean distance between the two
/// positions of two different indices.
/// </summary>
static long[,] ComputeEuclideanDistanceMatrix(in int[,] locations)
{
// Calculate the distance matrix using Euclidean distance.
int locationNumber = locations.GetLength(0);
long[,] distanceMatrix = new long[locationNumber, locationNumber];
for (int fromNode = 0; fromNode < locationNumber; fromNode++)
{
for (int toNode = 0; toNode < locationNumber; toNode++)
{
if (fromNode == toNode)
distanceMatrix[fromNode, toNode] = 0;
else
distanceMatrix[fromNode, toNode] =
(long)Math.Sqrt(Math.Pow(locations[toNode, 0] - locations[fromNode, 0], 2) +
Math.Pow(locations[toNode, 1] - locations[fromNode, 1], 2));
}
}
return distanceMatrix;
}
/// <summary>
/// Print the solution.
/// </summary>
static void PrintSolution(in RoutingModel routing, in RoutingIndexManager manager, in Assignment solution)
{
Console.WriteLine("Objective: {0}", solution.ObjectiveValue());
// Inspect solution.
Console.WriteLine("Route:");
long routeDistance = 0;
var index = routing.Start(0);
while (routing.IsEnd(index) == false)
{
Console.Write("{0} -> ", manager.IndexToNode((int)index));
var previousIndex = index;
index = solution.Value(routing.NextVar(index));
routeDistance += routing.GetArcCostForVehicle(previousIndex, index, 0);
}
Console.WriteLine("{0}", manager.IndexToNode((int)index));
Console.WriteLine("Route distance: {0}m", routeDistance);
}
public static void Main(String[] args)
{
// Instantiate the data problem.
DataModel data = new DataModel();
// Create Routing Index Manager
RoutingIndexManager manager =
new RoutingIndexManager(data.Locations.GetLength(0), data.VehicleNumber, data.Depot);
// Create Routing Model.
RoutingModel routing = new RoutingModel(manager);
// Define cost of each arc.
long[,] distanceMatrix = ComputeEuclideanDistanceMatrix(data.Locations);
int transitCallbackIndex = routing.RegisterTransitCallback((long fromIndex, long toIndex) =>
{
// Convert from routing variable Index to
// distance matrix NodeIndex.
var fromNode = manager.IndexToNode(fromIndex);
var toNode = manager.IndexToNode(toIndex);
return distanceMatrix[fromNode, toNode];
});
routing.SetArcCostEvaluatorOfAllVehicles(transitCallbackIndex);
// Setting first solution heuristic.
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
// Solve the problem.
Assignment solution = routing.SolveWithParameters(searchParameters);
// Print solution on console.
PrintSolution(routing, manager, solution);
}
}
Cómo cambiar la estrategia de búsqueda
El solucionador de enrutamiento no siempre muestra la solución óptima a un TSP, ya que los problemas de enrutamiento son intratables por cálculo. Por ejemplo, la solución que se mostró en el ejemplo anterior no es la ruta óptima.
Para encontrar una mejor solución, puedes usar una estrategia de búsqueda más avanzada, llamada búsqueda local guiada, que permite al agente de resolución escapar un mínimo local: una solución más corta que todas las rutas cercanas, pero que no es el mínimo global. Después de alejarse del mínimo local, el solucionador continúa la búsqueda.
En los siguientes ejemplos, se muestra cómo configurar una búsqueda local guiada para el ejemplo de la placa de circuito.
Python
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.local_search_metaheuristic = (
routing_enums_pb2.LocalSearchMetaheuristic.GUIDED_LOCAL_SEARCH)
search_parameters.time_limit.seconds = 30
search_parameters.log_search = True
C++
RoutingSearchParameters searchParameters = DefaultRoutingSearchParameters();
searchParameters.set_local_search_metaheuristic(
LocalSearchMetaheuristic::GUIDED_LOCAL_SEARCH);
searchParameters.mutable_time_limit()->set_seconds(30);
search_parameters.set_log_search(true);
Java
Agrega la siguiente instrucción `import` al comienzo del programa:import com.google.protobuf.Duration;Luego, configura los parámetros de búsqueda de la siguiente manera:
RoutingSearchParameters searchParameters =
main.defaultRoutingSearchParameters()
.toBuilder()
.setFirstSolutionStrategy(FirstSolutionStrategy.Value.PATH_CHEAPEST_ARC)
.setLocalSearchMetaheuristic(LocalSearchMetaheuristic.Value.GUIDED_LOCAL_SEARCH)
.setTimeLimit(Duration.newBuilder().setSeconds(30).build())
.setLogSearch(true)
.build();
C#
Agrega la siguiente línea al principio del programa:using Google.Protobuf.WellKnownTypes; // DurationLuego, configura los parámetros de búsqueda de la siguiente manera:
RoutingSearchParameters searchParameters =
operations_research_constraint_solver.DefaultRoutingSearchParameters();
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;
searchParameters.LocalSearchMetaheuristic = LocalSearchMetaheuristic.Types.Value.GuidedLocalSearch;
searchParameters.TimeLimit = new Duration { Seconds = 30 };
searchParameters.LogSearch = true;
Para ver otras estrategias de búsqueda local, consulta Opciones de búsqueda local.
Los ejemplos anteriores también habilitan el registro para la búsqueda. Si bien el registro no es obligatorio, puede ser útil para la depuración.
Cuando ejecutas el programa después de realizar los cambios anteriores, obtienes la siguiente solución, que es más corta que la solución que se muestra en la sección anterior.
Objective: 2672 Route: 0 -> 3 -> 276 -> 4 -> 5 -> 6 -> 8 -> 7 -> 9 -> 10 -> 11 -> 14 -> 12 -> 13 -> 23 -> 22 -> 24 -> 21 -> 25 -> 26 -> 27 -> 28 -> 125 -> 126 -> 127 -> 20 -> 19 -> 130 -> 129 -> 128 -> 153 -> 154 -> 152 -> 155 -> 151 -> 150 -> 177 -> 176 -> 175 -> 180 -> 161 -> 160 -> 174 -> 159 -> 158 -> 157 -> 156 -> 118 -> 119 -> 120 -> 121 -> 122 -> 123 -> 124 -> 29 -> 30 -> 31 -> 32 -> 33 -> 34 -> 35 -> 36 -> 37 -> 38 -> 39 -> 40 -> 41 -> 42 -> 59 -> 60 -> 58 -> 43 -> 44 -> 45 -> 46 -> 47 -> 48 -> 49 -> 50 -> 51 -> 52 -> 53 -> 54 -> 55 -> 56 -> 57 -> 67 -> 68 -> 66 -> 69 -> 70 -> 71 -> 72 -> 73 -> 75 -> 74 -> 76 -> 77 -> 78 -> 80 -> 81 -> 88 -> 79 -> 92 -> 93 -> 94 -> 95 -> 96 -> 97 -> 98 -> 99 -> 100 -> 101 -> 102 -> 91 -> 90 -> 89 -> 108 -> 111 -> 87 -> 82 -> 83 -> 86 -> 112 -> 115 -> 85 -> 84 -> 64 -> 65 -> 63 -> 62 -> 61 -> 117 -> 116 -> 114 -> 113 -> 110 -> 109 -> 107 -> 103 -> 104 -> 105 -> 106 -> 173 -> 172 -> 171 -> 170 -> 169 -> 168 -> 167 -> 166 -> 165 -> 164 -> 163 -> 162 -> 187 -> 188 -> 189 -> 190 -> 191 -> 192 -> 185 -> 186 -> 184 -> 183 -> 182 -> 181 -> 179 -> 178 -> 149 -> 148 -> 138 -> 137 -> 136 -> 266 -> 267 -> 135 -> 134 -> 268 -> 269 -> 133 -> 132 -> 131 -> 18 -> 17 -> 16 -> 15 -> 270 -> 271 -> 272 -> 273 -> 274 -> 275 -> 259 -> 258 -> 260 -> 261 -> 262 -> 263 -> 264 -> 265 -> 139 -> 140 -> 147 -> 146 -> 141 -> 142 -> 145 -> 144 -> 198 -> 197 -> 196 -> 193 -> 194 -> 195 -> 200 -> 201 -> 199 -> 143 -> 202 -> 203 -> 204 -> 205 -> 206 -> 207 -> 252 -> 253 -> 256 -> 257 -> 255 -> 254 -> 251 -> 208 -> 209 -> 210 -> 211 -> 212 -> 213 -> 214 -> 215 -> 216 -> 217 -> 218 -> 219 -> 220 -> 221 -> 222 -> 223 -> 224 -> 225 -> 226 -> 227 -> 232 -> 233 -> 234 -> 235 -> 236 -> 237 -> 230 -> 231 -> 228 -> 229 -> 250 -> 245 -> 238 -> 239 -> 240 -> 241 -> 242 -> 243 -> 244 -> 246 -> 249 -> 248 -> 247 -> 277 -> 278 -> 2 -> 279 -> 1 -> 0
Para obtener más opciones de búsqueda, consulta Opciones de enrutamiento.
Los mejores algoritmos ahora pueden resolver de forma rutinaria las instancias de TSP con decenas de miles de nodos. (El registro al momento de escribir es la instancia pla85900 en TSPLIB, una aplicación de VLSI con 85,900 nodos. Para ciertas instancias con millones de nodos, se comprobó que las soluciones se encuentran dentro del 1% de un recorrido óptimo).
Escala la matriz de distancia
Dado que el solucionador de enrutamiento funciona en los números enteros, si tu matriz de distancia tiene entradas que no sean números enteros, debes redondear las distancias a números enteros. Si algunas distancias son pequeñas, el redondeo puede afectar la solución.
Para evitar cualquier problema con el redondeo, puedes scale: la matriz de distancia: multiplica todas las entradas de la matriz por un número grande, por ejemplo, 100. Esto multiplica la longitud de cualquier ruta por un factor de 100, pero no cambia la solución. La ventaja es que cuando redondeas las entradas de la matriz, la cantidad de redondeo (que es, como máximo, 0.5) es muy pequeña en comparación con las distancias, por lo que no afectará significativamente la solución.
Si escalas la matriz de distancia, también debes cambiar la impresora de la solución para dividir las longitudes de ruta escaladas por el factor de escalamiento, de modo que muestre las distancias sin ajustar de las rutas.
