Di bagian berikut, kami akan menggambarkan {i>constraint programming <i}(CP) dengan masalah gabungan berdasarkan permainan catur. Dalam permainan catur, ratu bisa menyerang secara horizontal, vertikal, dan diagonal. Masalah N-queens menanyakan:
Bagaimana ratu N ditempatkan di papan catur NxN sehingga tidak ada dua ratu yang menyerang sama lain?
Di bawah ini, Anda dapat melihat satu kemungkinan solusi untuk masalah N-queens untuk N = 4.
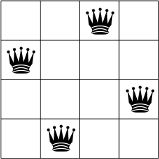
Tidak ada dua ratu yang berada di baris, kolom, atau diagonal yang sama.
Perhatikan bahwa ini bukan masalah pengoptimalan: kami ingin menemukan semua sebuah solusi, bukan satu solusi optimal, yang menjadikannya kandidat alami untuk pemrograman kendala. Bagian berikut ini menjelaskan pendekatan CP untuk masalah N-queens, dan menyajikan program yang menyelesaikannya menggunakan pemecah masalah CP-SAT dan pemecah masalah.
Pendekatan CP terhadap masalah N-queens
Pemecah masalah CP bekerja dengan secara sistematis mencoba semua kemungkinan penugasan nilai ke variabel-variabel dalam masalah, untuk menemukan solusi yang layak. Pada soal 4-queen, pemecah soal dimulai dari posisi paling kiri dan berturut-turut menempatkan satu ratu di setiap kolom, di lokasi yang tidak diserang oleh ratu yang ditempatkan sebelumnya.
Penyebaran dan backtracking
Ada dua elemen kunci untuk pencarian pemrograman batasan:
- Propagasi — Setiap kali pemecah masalah menetapkan nilai ke variabel, menambahkan batasan pada nilai yang mungkin dari variabel. Batasan ini disebarkan ke penetapan variabel mendatang. Misalnya, dalam soal 4-queens, setiap kali pemecah soal menempatkan ratu, tidak dapat menempatkan ratu lain pada baris dan diagonal tempat ratu saat ini berada. Penyebaran dapat mempercepat pencarian secara signifikan dengan mengurangi nilai-nilai variabel yang harus dijelajahi oleh pemecah masalah.
- Backtracking terjadi saat pemecah masalah tidak dapat menetapkan nilai ke variabel, karena kendala, atau menemukan solusi. Dalam kedua kasus tersebut, pemecah masalah kembali ke tahap sebelumnya dan mengubah nilai variabel di tahapan tersebut dengan nilai yang belum dicoba. Dalam contoh 4-queens, ini berarti memindahkan ratu ke persegi baru di kolom saat ini.
Selanjutnya, Anda akan melihat bagaimana {i>constraint programming<i} menggunakan propagasi dan {i>backtracking<i} untuk menyelesaikan soal 4-queens.
Misalkan pemecah soal memulai dengan secara bebas menempatkan queen di kiri atas kanan atas. Itu semacam hipotesis; mungkin ternyata tidak ada solusi dengan simbol ratu di sudut kiri atas.
Berdasarkan hipotesis ini, batasan apa yang dapat kita terapkan? Salah satu kendalanya adalah hanya boleh ada satu ratu di kolom (tanda X abu-abu di bawah), dan satu lagi membatasi dua ratu pada diagonal yang sama (X merah di bawah).
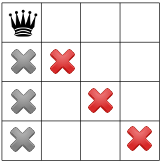
Batasan ketiga kami melarang ratu di baris yang sama:
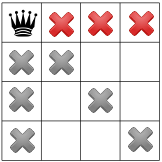
Batasan kita disebarkan, kita dapat menguji hipotesis lain, dan ratu kedua di salah satu kotak yang tersisa. Pemecah masalah kita mungkin memutuskan untuk menempatkannya di kotak pertama yang tersedia di kolom kedua:
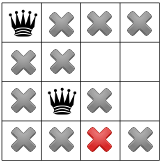
Setelah menyebarkan batasan diagonal, kita dapat melihat bahwa kotak yang tersedia di kolom ketiga atau baris terakhir:
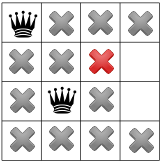
Karena tidak ada solusi yang mungkin dilakukan pada tahap ini, kita harus mundur. Salah satu pilihannya adalah pemecah masalah memilih kuadrat lain yang tersedia di kolom kedua. Namun, propagasi batasan kemudian memaksa ratu ke baris kedua kolom ketiga, tidak menyisakan tempat yang valid untuk ratu keempat:

Jadi pemecah masalah harus kembali lagi, kali ini kembali ke penempatan ratu pertama. Kita sekarang telah menunjukkan bahwa tidak ada solusi untuk ratu akan menempati persegi sudut.
Karena tidak ada ratu di sudut, pemecah soal menggerakkan ratu pertama ke bawah dengan satu, dan menyebar, hanya menyisakan satu tempat untuk ratu kedua:
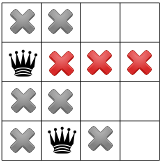
Propagasi lagi menunjukkan hanya satu tempat yang tersisa untuk ratu ketiga:
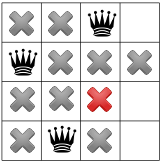
Dan untuk ratu keempat dan terakhir:

Kami memiliki solusi pertama kami! Jika kita menginstruksikan pemecah soal untuk berhenti setelah menemukan solusi pertama, semuanya akan berakhir di sini. Jika tidak, sistem akan mundur lagi dan menempatkan ratu pertama di baris ketiga kolom pertama.
Solusi menggunakan CP-SAT
Masalah N-queens idealnya sesuai untuk pemrograman batasan. Di sini kita akan membahas program Python singkat yang menggunakan pemecah masalah CP-SAT untuk menemukan semua solusi untuk masalah tersebut.
Mengimpor library
Kode berikut akan mengimpor library yang diperlukan.
Python
import sys import time from ortools.sat.python import cp_model
C++
#include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h"
Java
import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr;
C#
using System; using Google.OrTools.Sat;
Mendeklarasikan model
Kode berikut mendeklarasikan model CP-SAT.
Python
model = cp_model.CpModel()
C++
CpModelBuilder cp_model;
Java
CpModel model = new CpModel();
C#
CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
Membuat variabel
Pemecah soal membuat variabel untuk soal tersebut sebagai array bernama queens.
Python
# There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]
C++
// There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); }
Java
int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); }
C#
int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); }
Di sini kita asumsikan bahwa queens[j] adalah nomor baris untuk ratu di kolom j.
Dengan kata lain, queens[j] = i berarti ada ratu di baris i dan kolom j.
Membuat batasan
Berikut adalah kode yang membuat pembatas untuk masalah tersebut.
Python
# All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size))
C++
// The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2);
Java
// All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2);
C#
// All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2);
Kode ini menggunakan metode AddAllDifferent, yang memerlukan semua elemen
{i>array<i} variabel menjadi berbeda.
Mari kita lihat bagaimana batasan ini menjamin tiga kondisi untuk N-queens masalah (ratu pada baris, kolom, dan diagonal yang berbeda).
Tidak ada dua ratu di baris yang sama
Menerapkan metode AllDifferent pemecah ke queens akan memaksa nilai
queens[j] berbeda untuk setiap j, yang berarti semua ratu harus berada
baris yang berbeda.
Tidak ada dua ratu di kolom yang sama
Batasan ini bersifat implisit dalam definisi queens.
Karena tidak ada dua elemen queens yang dapat memiliki indeks yang sama, tidak ada dua ratu yang dapat
di kolom yang sama.
Tidak ada dua ratu pada diagonal yang sama
Batasan diagonal sedikit lebih rumit daripada batasan baris dan kolom. Pertama, jika dua ratu berbaring pada diagonal yang sama, maka salah satu dari kondisi berikut harus benar:
- Nomor baris ditambah nomor kolom untuk masing-masing ratu sama.
Dengan kata lain,
queens(j) + jmemiliki nilai yang sama untuk dua indeks yang berbedaj. - Nomor baris dikurangi nomor kolom untuk masing-masing dua ratu sama.
Dalam hal ini,
queens(j) - jmemiliki nilai yang sama untuk dua indeks yang berbedaj.
Salah satu kondisi ini berarti ratu berbaring pada diagonal menaik yang sama ( dari kiri ke kanan), sementara yang lain berarti mereka berbaring di posisi yang sama diagonal. Kondisi mana yang sesuai dengan naik dan turun tergantung pada bagaimana Anda mengatur baris dan kolom. Sebagaimana disebutkan dalam bagian sebelumnya, urutan tidak berpengaruh pada kumpulan solusi, hanya pada bagaimana Anda memvisualisasikannya.
Jadi, batasan diagonal adalah nilai queens(j) + j harus semuanya
berbeda, dan nilai-nilai queens(j) - j semua harus berbeda, agar
j yang berbeda.
Untuk menerapkan metode AddAllDifferent ke queens(j) + j, kita menempatkan instance N
variabel, untuk j dari 0 hingga N-1, ke dalam array, diag1, sebagai berikut:
q1 = model.NewIntVar(0, 2 * board_size, 'diag1_%i' % i) diag1.append(q1) model.Add(q1 == queens[j] + j)
Kemudian, kita menerapkan AddAllDifferent ke diag1.
model.AddAllDifferent(diag1)
Batasan untuk queens(j) - j dibuat dengan cara yang sama.
Membuat printer solusi
Untuk mencetak semua solusi masalah N-queens, Anda harus meneruskan callback, yang disebut printer solusi, ke pemecah CP-SAT. Callback mencetak setiap solusi baru yang ditemukan oleh pemecah masalah. Kode berikut membuat solusi {i>printer<i}.
Python
class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print()
C++
int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; }));
Java
static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; }
C#
public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; }
Perhatikan bahwa printer solusi harus ditulis sebagai class Python, karena Antarmuka Python ke pemecah masalah C++ yang mendasarinya.
Solusi dicetak dengan baris berikut di printer solusi.
for v in self.__variables: print('%s = %i' % (v, self.Value(v)), end = ' ')
Dalam contoh ini, self.__variables adalah variabel queens, dan setiap v
sesuai dengan salah satu dari delapan entri queens. Contoh ini mencetak solusi di
dalam format berikut: x0 = queens(0) x1 = queens(1) ... x7 = queens(7) dengan
xi adalah nomor kolom ratu di baris i.
Bagian berikutnya menunjukkan contoh solusi.
Memanggil pemecah masalah dan menampilkan hasilnya
Kode berikut menjalankan pemecah dan menampilkan solusinya.
Python
solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer)
C++
// Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions;
Java
CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb);
C#
// Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb);
Program ini menemukan 92 solusi berbeda untuk papan 8x8. Pertanyaan pertama.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Solutions found: 92Anda dapat menyelesaikan soal untuk papan dengan ukuran yang berbeda dengan meneruskan N sebagai
argumen command line. Misalnya, jika program diberi nama queens,
python nqueens_sat.py 6 memecahkan soal untuk papan 6x6.
Seluruh program
Berikut adalah keseluruhan program untuk program N-queens.
Python
"""OR-Tools solution to the N-queens problem.""" import sys import time from ortools.sat.python import cp_model class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() def main(board_size: int) -> None: # Creates the solver. model = cp_model.CpModel() # Creates the variables. # There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size)) # Solve the model. solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer) # Statistics. print("\nStatistics") print(f" conflicts : {solver.num_conflicts}") print(f" branches : {solver.num_branches}") print(f" wall time : {solver.wall_time} s") print(f" solutions found: {solution_printer.solution_count}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h" namespace operations_research { namespace sat { void NQueensSat(const int board_size) { // Instantiate the solver. CpModelBuilder cp_model; // There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2); int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; })); // Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions; // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << CpSolverResponseStats(response); } } // namespace sat } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { if (!absl::SimpleAtoi(argv[1], &board_size)) { LOG(INFO) << "Cannot parse '" << argv[1] << "', using the default value of 8."; board_size = 8; } } operations_research::sat::NQueensSat(board_size); return EXIT_SUCCESS; }
Java
package com.google.ortools.sat.samples; import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr; /** OR-Tools solution to the N-queens problem. */ public final class NQueensSat { static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; } public static void main(String[] args) { Loader.loadNativeLibraries(); // Create the model. CpModel model = new CpModel(); int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2); // Create a solver and solve the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb); // Statistics. System.out.println("Statistics"); System.out.println(" conflicts : " + solver.numConflicts()); System.out.println(" branches : " + solver.numBranches()); System.out.println(" wall time : " + solver.wallTime() + " s"); System.out.println(" solutions : " + cb.getSolutionCount()); } private NQueensSat() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.Sat; public class NQueensSat { public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; } static void Main() { // Constraint programming engine CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
Solusi menggunakan pemecah masalah TCP asli
Bagian berikut menampilkan program Python yang memecahkan N-queens menggunakan pemecah masalah TCP asli. (Namun, sebaiknya gunakan pemecah masalah CP-SAT yang lebih baru)
Mengimpor library
Kode berikut akan mengimpor library yang diperlukan.
Python
import sys from ortools.constraint_solver import pywrapcp
C++
#include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h"
Java
import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver;
C#
using System; using Google.OrTools.ConstraintSolver;
Mendeklarasikan pemecah
Kode berikut mendeklarasikan pemecah CP asli.
Python
solver = pywrapcp.Solver("n-queens")
C++
Solver solver("N-Queens");
Java
Solver solver = new Solver("N-Queens");
C#
Solver solver = new Solver("N-Queens");
Membuat variabel
Metode IntVar pemecah masalah membuat variabel untuk soal sebagai array
bernama queens.
Python
# The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]
C++
std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); }
Java
int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); }
C#
const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); }
Untuk solusi apa pun, queens[j] = i berarti ada ratu di kolom j dan baris
i.
Membuat batasan
Berikut adalah kode yang membuat pembatas untuk masalah tersebut.
Python
# All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))
C++
// The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2));
Java
// All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2));
C#
// All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent());
Batasan ini menjamin tiga kondisi untuk masalah N-queens ( ratu pada baris, kolom, dan diagonal yang berbeda).
Tidak ada dua ratu di baris yang sama
Menerapkan metode AllDifferent pemecah ke queens akan memaksa nilai
queens[j] berbeda untuk setiap j, yang berarti semua ratu harus berada
baris yang berbeda.
Tidak ada dua ratu di kolom yang sama
Batasan ini bersifat implisit dalam definisi queens.
Karena tidak ada dua elemen queens yang dapat memiliki indeks yang sama, tidak ada dua ratu yang dapat
di kolom yang sama.
Tidak ada dua ratu pada diagonal yang sama
Batasan diagonal sedikit lebih rumit daripada batasan baris dan kolom. Pertama, jika dua ratu terletak pada diagonal yang sama, salah satu hal berikut harus benar:
- Jika diagonal menurun (dari kiri ke kanan), angka baris ditambah
nomor kolom untuk masing-masing dari dua ratu sama. Jadi
queens(i) + imemiliki nilai yang sama untuk dua indeks yang berbedai. - Jika diagonal naik, nomor baris dikurangi nomor kolom untuk setiap
dari kedua ratu itu sama. Dalam hal ini,
queens(i) - imemiliki nilai yang sama untuk dua indeks yang berbedai.
Jadi, batasan diagonal adalah nilai queens(i) + i harus semuanya
berbeda, dan juga nilai-nilai queens(i) - i semua harus berbeda, untuk
i yang berbeda.
Kode di atas menambahkan batasan ini dengan menerapkan metode
AllDifferent
ke queens[j] + j dan queens[j] - j, untuk setiap i.
Menambahkan pembuat keputusan
Langkah selanjutnya adalah membuat pengambil keputusan, yang menetapkan strategi pencarian untuk masalah tersebut. Strategi penelusuran dapat berdampak besar pada waktu pencarian, karena penyebaran batasan, yang mengurangi jumlah nilai variabel dipelajari oleh pemecah soal. Anda sudah melihat contohnya di Contoh 4-queens.
Kode berikut membuat pembuat keputusan menggunakan
Phase
.
Python
db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
C++
DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);
Java
// Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
C#
// Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
Lihat Pembuat keputusan untuk mengetahui detail tentang
argumen input ke metode Phase.
Cara kerja pengambil keputusan dalam contoh 4-queens
Mari kita lihat bagaimana pembuat keputusan mengarahkan pencarian dalam
Contoh 4-queens.
Pemecah soal dimulai dengan queens[0], variabel pertama dalam array, seperti yang diarahkan
paling lambat CHOOSE_FIRST_UNBOUND. Pemecah masalah kemudian menetapkan queens[0] nilai terkecil
nilai yang belum dicoba, yaitu 0 pada tahap ini, seperti yang diarahkan oleh
ASSIGN_MIN_VALUE. Tindakan ini menempatkan ratu pertama di sudut kiri atas
papan.
Selanjutnya, pemecah masalah memilih queens[1], yang sekarang merupakan variabel tak terikat pertama dalam
queens. Setelah menerapkan batasan, ada dua kemungkinan baris untuk
queen di kolom 1: baris 2 atau baris 3. Opsi ASSIGN_MIN_VALUE mengarahkan
pemecah masalah untuk menetapkan queens[1] = 2. (Jika sebaliknya, Anda menetapkan IntValueStrategy ke
ASSIGN_MAX_VALUE, pemecah masalah akan menugaskan queens[1] = 3.)
Anda dapat memeriksa bahwa penelusuran lainnya mengikuti aturan yang sama.
Memanggil pemecah masalah dan menampilkan hasilnya
Kode berikut menjalankan pemecah dan menampilkan solusinya.
Python
# Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch()
C++
// Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch();
Java
int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch();
C#
// Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch();
Berikut solusi pertama yang ditemukan oleh program untuk papan 8x8.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Statistics
failures: 304
branches: 790
wall time: 5 ms
Solutions found: 92Anda dapat menyelesaikan soal untuk papan dengan ukuran yang berbeda dengan meneruskan N sebagai
argumen command line. Misalnya, python nqueens_cp.py 6 menyelesaikan soal
untuk papan 6x6.
Seluruh program
Program lengkapnya ditampilkan di bawah ini.
Python
"""OR-Tools solution to the N-queens problem.""" import sys from ortools.constraint_solver import pywrapcp def main(board_size): # Creates the solver. solver = pywrapcp.Solver("n-queens") # Creates the variables. # The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)])) db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE) # Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch() # Statistics. print("\nStatistics") print(f" failures: {solver.Failures()}") print(f" branches: {solver.Branches()}") print(f" wall time: {solver.WallTime()} ms") print(f" Solutions found: {num_solutions}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h" namespace operations_research { void NQueensCp(const int board_size) { // Instantiate the solver. Solver solver("N-Queens"); std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2)); DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch(); // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << " failures: " << solver.failures(); LOG(INFO) << " branches: " << solver.branches(); LOG(INFO) << " wall time: " << solver.wall_time() << " ms"; LOG(INFO) << " Solutions found: " << num_solutions; } } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { board_size = std::atoi(argv[1]); } operations_research::NQueensCp(board_size); return EXIT_SUCCESS; }
Java
// OR-Tools solution to the N-queens problem. package com.google.ortools.constraintsolver.samples; import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver; /** N-Queens Problem. */ public final class NQueensCp { public static void main(String[] args) { Loader.loadNativeLibraries(); // Instantiate the solver. Solver solver = new Solver("N-Queens"); int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2)); // Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch(); // Statistics. System.out.println("Statistics"); System.out.println(" failures: " + solver.failures()); System.out.println(" branches: " + solver.branches()); System.out.println(" wall time: " + solver.wallTime() + "ms"); System.out.println(" Solutions found: " + solutionCount); } private NQueensCp() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.ConstraintSolver; public class NQueensCp { public static void Main(String[] args) { // Instantiate the solver. Solver solver = new Solver("N-Queens"); const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent()); // Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch(); // Statistics. Console.WriteLine("Statistics"); Console.WriteLine($" failures: {solver.Failures()}"); Console.WriteLine($" branches: {solver.Branches()}"); Console.WriteLine($" wall time: {solver.WallTime()} ms"); Console.WriteLine($" Solutions found: {SolutionCount}"); } }
Jumlah solusi
Jumlah solusi meningkat kira-kira secara eksponensial sesuai ukuran papan:
| Ukuran papan | Solusi | Waktu untuk menemukan semua solusi (md) |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 2 | 0 |
| 5 | 10 | 0 |
| 6 | 4 | 0 |
| 7 | 40 | 3 |
| 8 | 92 | 9 |
| 9 | 352 | 35 |
| 10 | 724 | 95 |
| 11 | 2680 | 378 |
| 12 | 14200 | 2198 |
| 13 | 73712 | 11628 |
| 14 | 365596 | 62427 |
| 15 | 2279184 | 410701 |
Banyak solusi hanyalah rotasi yang lain, dan sebuah teknik yang disebut simetri dapat digunakan untuk mengurangi jumlah komputasi yang dibutuhkan. Kami tidak menggunakan hal itu di sini; solusi kami di atas tidak dimaksudkan untuk menjadi cepat, hanya sederhana. Tentu saja, kita bisa membuatnya lebih cepat jika kita hanya ingin menemukan satu solusi, bukan semuanya: tidak lebih dari beberapa milidetik untuk ukuran papan hingga 50.
