N クイーン問題

次のセクションでは、制約プログラミング（CP）を チェスゲームに基づく組み合わせ問題です。チェスのクイーンは、 水平、垂直、対角線上に展開します。N クイーンズ問題では、

NxN のチェス盤に N 個のクイーンを置いて、二人から攻撃されないようにするには どうですか？

以下は、N = 4 の場合の N クイーン問題に対して、考えられる解の 1 つです。

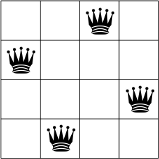
2 つのクイーンが同じ行、列、対角線上に存在することはできません。

なお、これは最適化の問題ではありません。 最適なソリューションではなく 制約プログラミングの考慮事項です 以降のセクションでは、N クイーン問題に対する CP のアプローチについて説明します。 CP-SAT ソルバーとオリジナルの CP を使って解くプログラムを提示する あります。

N クイーン問題に対する CP アプローチ

CP ソルバーは、体系的にすべてを試すことで機能する 問題内の変数への値の代入も考えられます。これにより、 具体的なソリューションを見ていきます。4 クイーン問題では、解法は左端から始まります。 各列にクイーンを 1 つずつ配置します。 過去に置かれたクイーンの攻撃を受けていません

伝播とバックトラック

制約プログラミングの検索には、次の 2 つの重要な要素があります。

• 伝播 - ソルバーが変数に値を割り当てるたびに、 制約を追加することで、割り当てられていないオブジェクトの 使用します。これらの制限は、今後の変数の割り当てにも反映されます。 たとえば、4 クイーン問題では、解法によってクイーンが 1 問出されるたびに、 他のクイーンをその行と対角線に配置することはできません。 伝播によって、一連の検出が減るため、検索が大幅に高速化されます。 変数値を求めます。
• バックトラッキングは、解法が次の値に値を代入できない場合に発生します。 変数に与えられるか、解答を見つけます。いずれの場合も、 バックトラックを行って前のステージにバックトラックし、 まだ試行されていない値に変更する必要があります。4 クイーンの例では、 つまり、クイーンを現在の列の新しい正方形に移動します。

次に、制約プログラミングが伝播とバックトラッキングを使用して、 クイーンの 4 つの問題を解きます

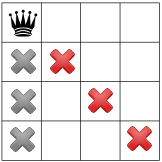
解法は、左上にクイーンを任意に配置することから始まります。 クリックします。これはある種の仮説で解決策がまったくないということが クイーンが左上に表示されます

この仮説を踏まえると、どのような制約を伝播できるでしょうか。制約の 1 つは、 1 つの列に 1 つのクイーン（下のグレーの X）しか存在せず、もう 1 つが 制約では、同じ対角線上に 2 つのクイーン（下の赤い X）を禁止します。

3 つ目の制約では、同じ行に対するクイーンを禁止します。

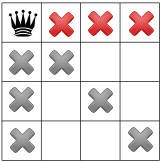
制約が伝播したら、別の仮説を検証して、 残りの正方形の 1 つに 2 番目のクイーンを表示します解法は 2 列目に使用可能な最初の正方形に配置します。

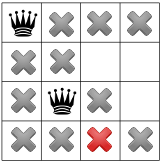
対角線の制約を伝播すると、制約が 使用可能な正方形を 3 列目か最終行に配置し、

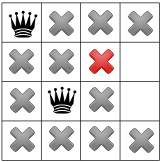
この段階では解決策が一切ないため、後戻りする必要があります。選択肢の一つとして 2 列目に利用可能なもう 1 つの正方形を選択します。 ただし、制約が伝播されると、クイーンは 4 番目のクイーンに有効なスポットが残っていないとします。

そのため、ソルバーは再びバックトラックを行う必要があり、 配置することにしましたクイーンたちの解決策は 隅の正方形が占有されることになります。

隅にクイーンはいないので、解法によって最初のクイーンが下に移動する。 2 番目のクイーンは 1 つのスポットしか残しません。

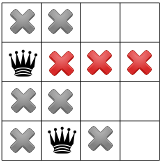
さらに伝播すると、3 人目のクイーンにはあと 1 つしか残っていないことがわかります。

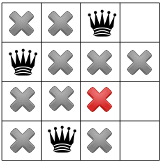
最後の 4 人目のクイーンは、

最初の解決策があります！見つけた後、ソルバーに指示を出して 終わりではありません。そうしないと、再度バックトラックが発生し、 最初のクイーンを最初の列の 3 行目に配置します。

CP-SAT を使用したソリューション

N クイーン問題は、制約プログラミングに適しています。この セクションでは、CP-SAT ソルバーを使用して 見つける必要があります。

ライブラリのインポート

次のコードは、必要なライブラリをインポートします。

Python

import sys
import time
from ortools.sat.python import cp_model

C++

#include <stdlib.h>

#include <sstream>
#include <string>
#include <vector>

#include "absl/strings/numbers.h"
#include "ortools/base/logging.h"
#include "ortools/sat/cp_model.h"
#include "ortools/sat/cp_model.pb.h"
#include "ortools/sat/cp_model_solver.h"
#include "ortools/sat/model.h"
#include "ortools/sat/sat_parameters.pb.h"
#include "ortools/util/sorted_interval_list.h"

Java

import com.google.ortools.Loader;
import com.google.ortools.sat.CpModel;
import com.google.ortools.sat.CpSolver;
import com.google.ortools.sat.CpSolverSolutionCallback;
import com.google.ortools.sat.IntVar;
import com.google.ortools.sat.LinearExpr;

C#

using System;
using Google.OrTools.Sat;

モデルを宣言する

次のコードは CP-SAT モデルを宣言しています。

Python

model = cp_model.CpModel()

C++

CpModelBuilder cp_model;

Java

CpModel model = new CpModel();

C#

        CpModel model = new CpModel();

        int BoardSize = 8;
        // There are `BoardSize` number of variables, one for a queen in each
        // column of the board. The value of each variable is the row that the
        // queen is in.
        IntVar[] queens = new IntVar[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
        }

        // Define constraints.
        // All rows must be different.
        model.AddAllDifferent(queens);

        // No two queens can be on the same diagonal.
        LinearExpr[] diag1 = new LinearExpr[BoardSize];
        LinearExpr[] diag2 = new LinearExpr[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
            diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
        }

        model.AddAllDifferent(diag1);
        model.AddAllDifferent(diag2);

        // Creates a solver and solves the model.
        CpSolver solver = new CpSolver();
        SolutionPrinter cb = new SolutionPrinter(queens);
        // Search for all solutions.
        solver.StringParameters = "enumerate_all_solutions:true";
        // And solve.
        solver.Solve(model, cb);

        Console.WriteLine("Statistics");
        Console.WriteLine($"  conflicts : {solver.NumConflicts()}");
        Console.WriteLine($"  branches  : {solver.NumBranches()}");
        Console.WriteLine($"  wall time : {solver.WallTime()} s");
        Console.WriteLine($"  number of solutions found: {cb.SolutionCount()}");
    }
}

変数を作成する

解法は、問題の変数を queens という名前の配列として作成します。

Python

# There are `board_size` number of variables, one for a queen in each column
# of the board. The value of each variable is the row that the queen is in.
queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]

C++

// There are `board_size` number of variables, one for a queen in each column
// of the board. The value of each variable is the row that the queen is in.
std::vector<IntVar> queens;
queens.reserve(board_size);
Domain range(0, board_size - 1);
for (int i = 0; i < board_size; ++i) {
  queens.push_back(
      cp_model.NewIntVar(range).WithName("x" + std::to_string(i)));
}

Java

int boardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each column of the board. The
// value of each variable is the row that the queen is in.
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
  queens[i] = model.newIntVar(0, boardSize - 1, "x" + i);
}

C#

int BoardSize = 8;
// There are `BoardSize` number of variables, one for a queen in each
// column of the board. The value of each variable is the row that the
// queen is in.
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
    queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
}

ここでは、queens[j] が列 j のクイーンの行番号であると仮定します。 つまり、queens[j] = i は、行 i、列 j にクイーンが存在することを意味します。

注: ソリューションの図を描くと、 行の順序が下から上か上から下か（ 列の順番が左から右か、その逆か）を指定します。ただし、 順序を変えても、可能性のあるすべての解法が変わるわけではなく、単純に 図に示しています。

制約を作成する

以下は、問題の制約を作成するコードです。

Python

# All rows must be different.
model.add_all_different(queens)

# No two queens can be on the same diagonal.
model.add_all_different(queens[i] + i for i in range(board_size))
model.add_all_different(queens[i] - i for i in range(board_size))

C++

// The following sets the constraint that all queens are in different rows.
cp_model.AddAllDifferent(queens);

// No two queens can be on the same diagonal.
std::vector<LinearExpr> diag_1;
diag_1.reserve(board_size);
std::vector<LinearExpr> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
  diag_1.push_back(queens[i] + i);
  diag_2.push_back(queens[i] - i);
}
cp_model.AddAllDifferent(diag_1);
cp_model.AddAllDifferent(diag_2);

Java

// All rows must be different.
model.addAllDifferent(queens);

// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[boardSize];
LinearExpr[] diag2 = new LinearExpr[boardSize];
for (int i = 0; i < boardSize; ++i) {
  diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build();
  diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build();
}
model.addAllDifferent(diag1);
model.addAllDifferent(diag2);

C#

// All rows must be different.
model.AddAllDifferent(queens);

// No two queens can be on the same diagonal.
LinearExpr[] diag1 = new LinearExpr[BoardSize];
LinearExpr[] diag2 = new LinearExpr[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
    diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
    diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
}

model.AddAllDifferent(diag1);
model.AddAllDifferent(diag2);

このコードは AddAllDifferent メソッドを使用します。このメソッドは、 異なる値にするためです。

これらの制約によって N クイーンの 3 つの条件がどのように保証されるかを見てみましょう。 （異なる行、列、対角線上のクイーン）。

同じ行に 2 人のクイーンは存在しない

ソルバーの AllDifferent メソッドを queens に適用すると、 queens[j] は j ごとに異なる。つまり、すべてのクイーンが 表示されます

同じ列に 2 つのクイーンがない

この制約は、queens の定義に暗黙的に含まれています。 queens の 2 つの要素に同じインデックスを設定できないため、2 つのクイーンを 表示されます

同じ対角線上に 2 つのクイーンはない

対角線の制約は、行と列の制約よりも少し複雑です。 まず、2 つのクイーンが同じ対角線上にある場合、次の条件のいずれかになります。 次の条件を満たしている必要があります。

• 2 つのクイーンのそれぞれの行番号と列番号は等しくなります。 つまり、queens(j) + j は 2 つの異なるインデックスに同じ値を持ちます。 j。
• 2 つのクイーンのそれぞれの行番号から列番号を引いた値は等しくなります。 この場合、queens(j) - j は 2 つの異なるインデックス j に同じ値を持ちます。

これらの条件のいずれかは、クイーンが同じ昇順対角線上に位置していることを意味します（ もう 1 つは同じ降順であることを表します。 対角線上。どの条件が昇順に対応し、どの条件が降順に対応するか 行と列の順序によって異なります。第 2 部の 前のセクションをご覧ください。順序は 可視化する方法を見ていきます。

したがって、対角線の制約は queens(j) + j の値がすべて また、queens(j) - j の値は、すべて異なる必要があります。 異なる j。

AddAllDifferent メソッドを queens(j) + j に適用するには、N 個のインスタンスを 変数の 0 から N-1 までの j を、次のように配列 diag1 に変換します。

q1 = model.NewIntVar(0, 2 * board_size, 'diag1_%i' % i)
diag1.append(q1)
model.Add(q1 == queens[j] + j)

次に、AddAllDifferent を diag1 に適用します。

model.AddAllDifferent(diag1)

queens(j) - j の制約も同様に作成されます。

ソリューション プリンタを作成

N クイーン問題の全解を出力するには、 ソリューション プリンタと呼ばれます。コールバックは、 解き明かします次のコードは、 あります。

Python

class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback):
    """Print intermediate solutions."""

    def __init__(self, queens: list[cp_model.IntVar]):
        cp_model.CpSolverSolutionCallback.__init__(self)
        self.__queens = queens
        self.__solution_count = 0
        self.__start_time = time.time()

    @property
    def solution_count(self) -> int:
        return self.__solution_count

    def on_solution_callback(self):
        current_time = time.time()
        print(
            f"Solution {self.__solution_count}, "
            f"time = {current_time - self.__start_time} s"
        )
        self.__solution_count += 1

        all_queens = range(len(self.__queens))
        for i in all_queens:
            for j in all_queens:
                if self.value(self.__queens[j]) == i:
                    # There is a queen in column j, row i.
                    print("Q", end=" ")
                else:
                    print("_", end=" ")
            print()
        print()

C++

int num_solutions = 0;
Model model;
model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) {
  LOG(INFO) << "Solution " << num_solutions;
  for (int i = 0; i < board_size; ++i) {
    std::stringstream ss;
    for (int j = 0; j < board_size; ++j) {
      if (SolutionIntegerValue(response, queens[j]) == i) {
        // There is a queen in column j, row i.
        ss << "Q";
      } else {
        ss << "_";
      }
      if (j != board_size - 1) ss << " ";
    }
    LOG(INFO) << ss.str();
  }
  num_solutions++;
}));

Java

static class SolutionPrinter extends CpSolverSolutionCallback {
  public SolutionPrinter(IntVar[] queensIn) {
    solutionCount = 0;
    queens = queensIn;
  }

  @Override
  public void onSolutionCallback() {
    System.out.println("Solution " + solutionCount);
    for (int i = 0; i < queens.length; ++i) {
      for (int j = 0; j < queens.length; ++j) {
        if (value(queens[j]) == i) {
          System.out.print("Q");
        } else {
          System.out.print("_");
        }
        if (j != queens.length - 1) {
          System.out.print(" ");
        }
      }
      System.out.println();
    }
    solutionCount++;
  }

  public int getSolutionCount() {
    return solutionCount;
  }

  private int solutionCount;
  private final IntVar[] queens;
}

C#

public class SolutionPrinter : CpSolverSolutionCallback
{
    public SolutionPrinter(IntVar[] queens)
    {
        queens_ = queens;
    }

    public override void OnSolutionCallback()
    {
        Console.WriteLine($"Solution {SolutionCount_}");
        for (int i = 0; i < queens_.Length; ++i)
        {
            for (int j = 0; j < queens_.Length; ++j)
            {
                if (Value(queens_[j]) == i)
                {
                    Console.Write("Q");
                }
                else
                {
                    Console.Write("_");
                }
                if (j != queens_.Length - 1)
                    Console.Write(" ");
            }
            Console.WriteLine("");
        }
        SolutionCount_++;
    }

    public int SolutionCount()
    {
        return SolutionCount_;
    }

    private int SolutionCount_;
    private IntVar[] queens_;
}

なお、解答作成装置は Python クラスとして記述する必要があります。これは、 基盤となる C++ ソルバーへの Python インターフェース。

解答は、解答プリンタに次の行によって印刷されます。

for v in self.__variables:
print('%s = %i' % (v, self.Value(v)), end = ' ')

この例では、self.__variables は変数 queens で、各 v は queens の 8 つのエントリの 1 つに対応します。これにより x0 = queens(0) x1 = queens(1) ... x7 = queens(7) の形式になります。 xi は、行 i のクイーンの列番号です。

次のセクションでは、ソリューションの例を示します。

ソルバーを呼び出して結果を表示する

次のコードはソルバーを実行し、解答を表示します。

Python

solver = cp_model.CpSolver()
solution_printer = NQueenSolutionPrinter(queens)
solver.parameters.enumerate_all_solutions = True
solver.solve(model, solution_printer)

C++

// Tell the solver to enumerate all solutions.
SatParameters parameters;
parameters.set_enumerate_all_solutions(true);
model.Add(NewSatParameters(parameters));

const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model);
LOG(INFO) << "Number of solutions found: " << num_solutions;

Java

CpSolver solver = new CpSolver();
SolutionPrinter cb = new SolutionPrinter(queens);
// Tell the solver to enumerate all solutions.
solver.getParameters().setEnumerateAllSolutions(true);
// And solve.
solver.solve(model, cb);

C#

// Creates a solver and solves the model.
CpSolver solver = new CpSolver();
SolutionPrinter cb = new SolutionPrinter(queens);
// Search for all solutions.
solver.StringParameters = "enumerate_all_solutions:true";
// And solve.
solver.Solve(model, cb);

このプログラムは、8x8 ボード用の 92 種類のソリューションを見つけます。それでは、最初の問題です。

        Q _ _ _ _ _ _ _
        _ _ _ _ _ _ Q _
        _ _ _ _ Q _ _ _
        _ _ _ _ _ _ _ Q
        _ Q _ _ _ _ _ _
        _ _ _ Q _ _ _ _
        _ _ _ _ _ Q _ _
        _ _ Q _ _ _ _ _
        ...91 other solutions displayed...
        Solutions found: 92

異なるサイズのボードの場合は、 コマンドライン引数を指定します。たとえば、プログラムの名前が queens の場合、 python nqueens_sat.py 6 は 6x6 ボードの問題を解決します。

プログラム全体

こちらが N-queens プログラムのプログラム全体です。

Python

"""OR-Tools solution to the N-queens problem."""
import sys
import time
from ortools.sat.python import cp_model


class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback):
    """Print intermediate solutions."""

    def __init__(self, queens: list[cp_model.IntVar]):
        cp_model.CpSolverSolutionCallback.__init__(self)
        self.__queens = queens
        self.__solution_count = 0
        self.__start_time = time.time()

    @property
    def solution_count(self) -> int:
        return self.__solution_count

    def on_solution_callback(self):
        current_time = time.time()
        print(
            f"Solution {self.__solution_count}, "
            f"time = {current_time - self.__start_time} s"
        )
        self.__solution_count += 1

        all_queens = range(len(self.__queens))
        for i in all_queens:
            for j in all_queens:
                if self.value(self.__queens[j]) == i:
                    # There is a queen in column j, row i.
                    print("Q", end=" ")
                else:
                    print("_", end=" ")
            print()
        print()



def main(board_size: int) -> None:
    # Creates the solver.
    model = cp_model.CpModel()

    # Creates the variables.
    # There are `board_size` number of variables, one for a queen in each column
    # of the board. The value of each variable is the row that the queen is in.
    queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]

    # Creates the constraints.
    # All rows must be different.
    model.add_all_different(queens)

    # No two queens can be on the same diagonal.
    model.add_all_different(queens[i] + i for i in range(board_size))
    model.add_all_different(queens[i] - i for i in range(board_size))

    # Solve the model.
    solver = cp_model.CpSolver()
    solution_printer = NQueenSolutionPrinter(queens)
    solver.parameters.enumerate_all_solutions = True
    solver.solve(model, solution_printer)

    # Statistics.
    print("\nStatistics")
    print(f"  conflicts      : {solver.num_conflicts}")
    print(f"  branches       : {solver.num_branches}")
    print(f"  wall time      : {solver.wall_time} s")
    print(f"  solutions found: {solution_printer.solution_count}")


if __name__ == "__main__":
    # By default, solve the 8x8 problem.
    size = 8
    if len(sys.argv) > 1:
        size = int(sys.argv[1])
    main(size)

C++

// OR-Tools solution to the N-queens problem.
#include <stdlib.h>

#include <sstream>
#include <string>
#include <vector>

#include "absl/strings/numbers.h"
#include "ortools/base/logging.h"
#include "ortools/sat/cp_model.h"
#include "ortools/sat/cp_model.pb.h"
#include "ortools/sat/cp_model_solver.h"
#include "ortools/sat/model.h"
#include "ortools/sat/sat_parameters.pb.h"
#include "ortools/util/sorted_interval_list.h"

namespace operations_research {
namespace sat {

void NQueensSat(const int board_size) {
  // Instantiate the solver.
  CpModelBuilder cp_model;

  // There are `board_size` number of variables, one for a queen in each column
  // of the board. The value of each variable is the row that the queen is in.
  std::vector<IntVar> queens;
  queens.reserve(board_size);
  Domain range(0, board_size - 1);
  for (int i = 0; i < board_size; ++i) {
    queens.push_back(
        cp_model.NewIntVar(range).WithName("x" + std::to_string(i)));
  }

  // Define constraints.
  // The following sets the constraint that all queens are in different rows.
  cp_model.AddAllDifferent(queens);

  // No two queens can be on the same diagonal.
  std::vector<LinearExpr> diag_1;
  diag_1.reserve(board_size);
  std::vector<LinearExpr> diag_2;
  diag_2.reserve(board_size);
  for (int i = 0; i < board_size; ++i) {
    diag_1.push_back(queens[i] + i);
    diag_2.push_back(queens[i] - i);
  }
  cp_model.AddAllDifferent(diag_1);
  cp_model.AddAllDifferent(diag_2);

  int num_solutions = 0;
  Model model;
  model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) {
    LOG(INFO) << "Solution " << num_solutions;
    for (int i = 0; i < board_size; ++i) {
      std::stringstream ss;
      for (int j = 0; j < board_size; ++j) {
        if (SolutionIntegerValue(response, queens[j]) == i) {
          // There is a queen in column j, row i.
          ss << "Q";
        } else {
          ss << "_";
        }
        if (j != board_size - 1) ss << " ";
      }
      LOG(INFO) << ss.str();
    }
    num_solutions++;
  }));

  // Tell the solver to enumerate all solutions.
  SatParameters parameters;
  parameters.set_enumerate_all_solutions(true);
  model.Add(NewSatParameters(parameters));

  const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model);
  LOG(INFO) << "Number of solutions found: " << num_solutions;

  // Statistics.
  LOG(INFO) << "Statistics";
  LOG(INFO) << CpSolverResponseStats(response);
}

}  // namespace sat
}  // namespace operations_research

int main(int argc, char** argv) {
  int board_size = 8;
  if (argc > 1) {
    if (!absl::SimpleAtoi(argv[1], &board_size)) {
      LOG(INFO) << "Cannot parse '" << argv[1]
                << "', using the default value of 8.";
      board_size = 8;
    }
  }
  operations_research::sat::NQueensSat(board_size);
  return EXIT_SUCCESS;
}

Java

package com.google.ortools.sat.samples;
import com.google.ortools.Loader;
import com.google.ortools.sat.CpModel;
import com.google.ortools.sat.CpSolver;
import com.google.ortools.sat.CpSolverSolutionCallback;
import com.google.ortools.sat.IntVar;
import com.google.ortools.sat.LinearExpr;

/** OR-Tools solution to the N-queens problem. */
public final class NQueensSat {
  static class SolutionPrinter extends CpSolverSolutionCallback {
    public SolutionPrinter(IntVar[] queensIn) {
      solutionCount = 0;
      queens = queensIn;
    }

    @Override
    public void onSolutionCallback() {
      System.out.println("Solution " + solutionCount);
      for (int i = 0; i < queens.length; ++i) {
        for (int j = 0; j < queens.length; ++j) {
          if (value(queens[j]) == i) {
            System.out.print("Q");
          } else {
            System.out.print("_");
          }
          if (j != queens.length - 1) {
            System.out.print(" ");
          }
        }
        System.out.println();
      }
      solutionCount++;
    }

    public int getSolutionCount() {
      return solutionCount;
    }

    private int solutionCount;
    private final IntVar[] queens;
  }

  public static void main(String[] args) {
    Loader.loadNativeLibraries();
    // Create the model.
    CpModel model = new CpModel();

    int boardSize = 8;
    // There are `BoardSize` number of variables, one for a queen in each column of the board. The
    // value of each variable is the row that the queen is in.
    IntVar[] queens = new IntVar[boardSize];
    for (int i = 0; i < boardSize; ++i) {
      queens[i] = model.newIntVar(0, boardSize - 1, "x" + i);
    }

    // Define constraints.
    // All rows must be different.
    model.addAllDifferent(queens);

    // No two queens can be on the same diagonal.
    LinearExpr[] diag1 = new LinearExpr[boardSize];
    LinearExpr[] diag2 = new LinearExpr[boardSize];
    for (int i = 0; i < boardSize; ++i) {
      diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build();
      diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build();
    }
    model.addAllDifferent(diag1);
    model.addAllDifferent(diag2);

    // Create a solver and solve the model.
    CpSolver solver = new CpSolver();
    SolutionPrinter cb = new SolutionPrinter(queens);
    // Tell the solver to enumerate all solutions.
    solver.getParameters().setEnumerateAllSolutions(true);
    // And solve.
    solver.solve(model, cb);

    // Statistics.
    System.out.println("Statistics");
    System.out.println("  conflicts : " + solver.numConflicts());
    System.out.println("  branches  : " + solver.numBranches());
    System.out.println("  wall time : " + solver.wallTime() + " s");
    System.out.println("  solutions : " + cb.getSolutionCount());
  }

  private NQueensSat() {}
}

C#

// OR-Tools solution to the N-queens problem.
using System;
using Google.OrTools.Sat;

public class NQueensSat
{
    public class SolutionPrinter : CpSolverSolutionCallback
    {
        public SolutionPrinter(IntVar[] queens)
        {
            queens_ = queens;
        }

        public override void OnSolutionCallback()
        {
            Console.WriteLine($"Solution {SolutionCount_}");
            for (int i = 0; i < queens_.Length; ++i)
            {
                for (int j = 0; j < queens_.Length; ++j)
                {
                    if (Value(queens_[j]) == i)
                    {
                        Console.Write("Q");
                    }
                    else
                    {
                        Console.Write("_");
                    }
                    if (j != queens_.Length - 1)
                        Console.Write(" ");
                }
                Console.WriteLine("");
            }
            SolutionCount_++;
        }

        public int SolutionCount()
        {
            return SolutionCount_;
        }

        private int SolutionCount_;
        private IntVar[] queens_;
    }

    static void Main()
    {
        // Constraint programming engine
        CpModel model = new CpModel();

        int BoardSize = 8;
        // There are `BoardSize` number of variables, one for a queen in each
        // column of the board. The value of each variable is the row that the
        // queen is in.
        IntVar[] queens = new IntVar[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}");
        }

        // Define constraints.
        // All rows must be different.
        model.AddAllDifferent(queens);

        // No two queens can be on the same diagonal.
        LinearExpr[] diag1 = new LinearExpr[BoardSize];
        LinearExpr[] diag2 = new LinearExpr[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i);
            diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i);
        }

        model.AddAllDifferent(diag1);
        model.AddAllDifferent(diag2);

        // Creates a solver and solves the model.
        CpSolver solver = new CpSolver();
        SolutionPrinter cb = new SolutionPrinter(queens);
        // Search for all solutions.
        solver.StringParameters = "enumerate_all_solutions:true";
        // And solve.
        solver.Solve(model, cb);

        Console.WriteLine("Statistics");
        Console.WriteLine($"  conflicts : {solver.NumConflicts()}");
        Console.WriteLine($"  branches  : {solver.NumBranches()}");
        Console.WriteLine($"  wall time : {solver.WallTime()} s");
        Console.WriteLine($"  number of solutions found: {cb.SolutionCount()}");
    }
}

元の CP ソルバーを使用した解

以降のセクションでは、N クイーンを 元の CP ソルバーです。 （ただし、新しい CP-SAT ソルバーの使用をおすすめします）。

ライブラリのインポート

次のコードは、必要なライブラリをインポートします。

Python

import sys
from ortools.constraint_solver import pywrapcp

C++

#include <cstdint>
#include <cstdlib>
#include <sstream>
#include <vector>

#include "ortools/base/logging.h"
#include "ortools/constraint_solver/constraint_solver.h"

Java

import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.DecisionBuilder;
import com.google.ortools.constraintsolver.IntVar;
import com.google.ortools.constraintsolver.Solver;

C#

using System;
using Google.OrTools.ConstraintSolver;

解法を宣言する

次のコードは、元の CP ソルバーを宣言しています。

Python

solver = pywrapcp.Solver("n-queens")

C++

Solver solver("N-Queens");

Java

Solver solver = new Solver("N-Queens");

C#

Solver solver = new Solver("N-Queens");

変数を作成する

解法の IntVar メソッドは、問題の変数を配列として作成する 名前は「queens」です。

Python

# The array index is the column, and the value is the row.
queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]

C++

std::vector<IntVar*> queens;
queens.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
  queens.push_back(
      solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i)));
}

Java

int boardSize = 8;
IntVar[] queens = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
  queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i);
}

C#

const int BoardSize = 8;
IntVar[] queens = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
    queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}");
}

どのような解でも、queens[j] = i は列 j と行にクイーンが存在することを意味します。 i。

制約を作成する

以下は、問題の制約を作成するコードです。

Python

# All rows must be different.
solver.Add(solver.AllDifferent(queens))

# No two queens can be on the same diagonal.
solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)]))
solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))

C++

// The following sets the constraint that all queens are in different rows.
solver.AddConstraint(solver.MakeAllDifferent(queens));

// All columns must be different because the indices of queens are all
// different. No two queens can be on the same diagonal.
std::vector<IntVar*> diag_1;
diag_1.reserve(board_size);
std::vector<IntVar*> diag_2;
diag_2.reserve(board_size);
for (int i = 0; i < board_size; ++i) {
  diag_1.push_back(solver.MakeSum(queens[i], i)->Var());
  diag_2.push_back(solver.MakeSum(queens[i], -i)->Var());
}
solver.AddConstraint(solver.MakeAllDifferent(diag_1));
solver.AddConstraint(solver.MakeAllDifferent(diag_2));

Java

// All rows must be different.
solver.addConstraint(solver.makeAllDifferent(queens));

// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[boardSize];
IntVar[] diag2 = new IntVar[boardSize];
for (int i = 0; i < boardSize; ++i) {
  diag1[i] = solver.makeSum(queens[i], i).var();
  diag2[i] = solver.makeSum(queens[i], -i).var();
}
solver.addConstraint(solver.makeAllDifferent(diag1));
solver.addConstraint(solver.makeAllDifferent(diag2));

C#

// All rows must be different.
solver.Add(queens.AllDifferent());

// All columns must be different because the indices of queens are all different.
// No two queens can be on the same diagonal.
IntVar[] diag1 = new IntVar[BoardSize];
IntVar[] diag2 = new IntVar[BoardSize];
for (int i = 0; i < BoardSize; ++i)
{
    diag1[i] = solver.MakeSum(queens[i], i).Var();
    diag2[i] = solver.MakeSum(queens[i], -i).Var();
}

solver.Add(diag1.AllDifferent());
solver.Add(diag2.AllDifferent());

これらの制約により、N クイーン問題（ 異なる行、列、対角線上のクイーンなど）が使用されます。

同じ行に 2 人のクイーンは存在しない

ソルバーの AllDifferent メソッドを queens に適用すると、 queens[j] は j ごとに異なる。つまり、すべてのクイーンが 表示されます

同じ列に 2 つのクイーンがない

この制約は、queens の定義に暗黙的に含まれています。 queens の 2 つの要素に同じインデックスを設定できないため、2 つのクイーンを 表示されます

同じ対角線上に 2 つのクイーンはない

対角線の制約は、行と列の制約よりも少し複雑です。 まず、2 つのクイーンが同じ対角線上にある場合、次のいずれかに該当する必要があります。

• 対角線が降順（左から右へ）の場合は、行番号と 2 つのクイーンの列番号は等しくなります。したがって、queens(i) + i には 2 つの異なるインデックス i に同じ値を設定しています。
• 対角線が昇順の場合は、それぞれの行番号から列番号を引いた値 等しくなります。この場合、queens(i) - i は同じ値になります。 （2 つの異なるインデックス i に対して）

したがって、対角線の制約は queens(i) + i の値がすべて 同じく、queens(i) - i の値もすべて異なっている必要があります。 異なる i。

上記のコードでは、この制約を追加するために、 AllDifferent メソッドを i ごとに queens[j] + j と queens[j] - j に渡します。

意思決定者を追加する

次のステップでは、意思決定者を作成して検索戦略を設定します。 解決します検索戦略は検索時間に大きな影響を与えます。 制約の伝播によって生じる変数値の数が減るため、 解明が必要なことです。この例については、このモジュールの 4 クイーンの例

次のコードは、ソルバーの Phase メソッドを呼び出します。

Python

db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)

C++

DecisionBuilder* const db = solver.MakePhase(
    queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);

Java

// Create the decision builder to search for solutions.
final DecisionBuilder db =
    solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);

C#

// Create the decision builder to search for solutions.
DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);

詳細はディシジョン ビルダーを参照 入力引数を Phase メソッドに渡します。

4 クイーンのサンプルにおける意思決定者の仕組み

では、意思決定者がどのように検索を指示するのかを 4 クイーンの例 指示どおり、解は配列の最初の変数である queens[0] で始まります 作成者: CHOOSE_FIRST_UNBOUND。解法は、queens[0] に最小値を 値（この段階では 0）を返します。 ASSIGN_MIN_VALUE。これにより、最初のクイーンがページの左上に配置され、 表示されます。

次に、ソルバーは queens[1] を選択します。これは、今度は最初の未バインドの変数です。 queens。制約を伝播すると、行が 2 つになり、 クイーンを列 1: 行 2 または行 3 に配置します。ASSIGN_MIN_VALUE オプションは、 queens[1] = 2 を割り当てます。（代わりに IntValueStrategy を ASSIGN_MAX_VALUE の場合は、ソルバーによって queens[1] = 3 が割り当てられます）。

残りの検索が同じルールに従っていることを確認できます。

ソルバーを呼び出して結果を表示する

次のコードはソルバーを実行し、解答を表示します。

Python

# Iterates through the solutions, displaying each.
num_solutions = 0
solver.NewSearch(db)
while solver.NextSolution():
    # Displays the solution just computed.
    for i in range(board_size):
        for j in range(board_size):
            if queens[j].Value() == i:
                # There is a queen in column j, row i.
                print("Q", end=" ")
            else:
                print("_", end=" ")
        print()
    print()
    num_solutions += 1
solver.EndSearch()

C++

// Iterates through the solutions, displaying each.
int num_solutions = 0;

solver.NewSearch(db);
while (solver.NextSolution()) {
  // Displays the solution just computed.
  LOG(INFO) << "Solution " << num_solutions;
  for (int i = 0; i < board_size; ++i) {
    std::stringstream ss;
    for (int j = 0; j < board_size; ++j) {
      if (queens[j]->Value() == i) {
        // There is a queen in column j, row i.
        ss << "Q";
      } else {
        ss << "_";
      }
      if (j != board_size - 1) ss << " ";
    }
    LOG(INFO) << ss.str();
  }
  num_solutions++;
}
solver.EndSearch();

Java

int solutionCount = 0;
solver.newSearch(db);
while (solver.nextSolution()) {
  System.out.println("Solution " + solutionCount);
  for (int i = 0; i < boardSize; ++i) {
    for (int j = 0; j < boardSize; ++j) {
      if (queens[j].value() == i) {
        System.out.print("Q");
      } else {
        System.out.print("_");
      }
      if (j != boardSize - 1) {
        System.out.print(" ");
      }
    }
    System.out.println();
  }
  solutionCount++;
}
solver.endSearch();

C#

// Iterates through the solutions, displaying each.
int SolutionCount = 0;
solver.NewSearch(db);
while (solver.NextSolution())
{
    Console.WriteLine("Solution " + SolutionCount);
    for (int i = 0; i < BoardSize; ++i)
    {
        for (int j = 0; j < BoardSize; ++j)
        {
            if (queens[j].Value() == i)
            {
                Console.Write("Q");
            }
            else
            {
                Console.Write("_");
            }
            if (j != BoardSize - 1)
                Console.Write(" ");
        }
        Console.WriteLine("");
    }
    SolutionCount++;
}
solver.EndSearch();

8x8 ボード用のプログラムで見つかった最初の解答は次のとおりです。

        Q _ _ _ _ _ _ _
        _ _ _ _ _ _ Q _
        _ _ _ _ Q _ _ _
        _ _ _ _ _ _ _ Q
        _ Q _ _ _ _ _ _
        _ _ _ Q _ _ _ _
        _ _ _ _ _ Q _ _
        _ _ Q _ _ _ _ _
        ...91 other solutions displayed...
        Statistics
        failures: 304
        branches: 790
        wall time: 5 ms
        Solutions found: 92

異なるサイズのボードの場合は、 コマンドライン引数を指定します。たとえば、python nqueens_cp.py 6 は問題を解決します。 6x6 のボードなら

プログラム全体

完全なプログラムを以下に示します。

Python

"""OR-Tools solution to the N-queens problem."""
import sys
from ortools.constraint_solver import pywrapcp


def main(board_size):
    # Creates the solver.
    solver = pywrapcp.Solver("n-queens")

    # Creates the variables.
    # The array index is the column, and the value is the row.
    queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]

    # Creates the constraints.
    # All rows must be different.
    solver.Add(solver.AllDifferent(queens))

    # No two queens can be on the same diagonal.
    solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)]))
    solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))

    db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)

    # Iterates through the solutions, displaying each.
    num_solutions = 0
    solver.NewSearch(db)
    while solver.NextSolution():
        # Displays the solution just computed.
        for i in range(board_size):
            for j in range(board_size):
                if queens[j].Value() == i:
                    # There is a queen in column j, row i.
                    print("Q", end=" ")
                else:
                    print("_", end=" ")
            print()
        print()
        num_solutions += 1
    solver.EndSearch()

    # Statistics.
    print("\nStatistics")
    print(f"  failures: {solver.Failures()}")
    print(f"  branches: {solver.Branches()}")
    print(f"  wall time: {solver.WallTime()} ms")
    print(f"  Solutions found: {num_solutions}")


if __name__ == "__main__":
    # By default, solve the 8x8 problem.
    size = 8
    if len(sys.argv) > 1:
        size = int(sys.argv[1])
    main(size)

C++

// OR-Tools solution to the N-queens problem.
#include <cstdint>
#include <cstdlib>
#include <sstream>
#include <vector>

#include "ortools/base/logging.h"
#include "ortools/constraint_solver/constraint_solver.h"

namespace operations_research {

void NQueensCp(const int board_size) {
  // Instantiate the solver.
  Solver solver("N-Queens");

  std::vector<IntVar*> queens;
  queens.reserve(board_size);
  for (int i = 0; i < board_size; ++i) {
    queens.push_back(
        solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i)));
  }

  // Define constraints.
  // The following sets the constraint that all queens are in different rows.
  solver.AddConstraint(solver.MakeAllDifferent(queens));

  // All columns must be different because the indices of queens are all
  // different. No two queens can be on the same diagonal.
  std::vector<IntVar*> diag_1;
  diag_1.reserve(board_size);
  std::vector<IntVar*> diag_2;
  diag_2.reserve(board_size);
  for (int i = 0; i < board_size; ++i) {
    diag_1.push_back(solver.MakeSum(queens[i], i)->Var());
    diag_2.push_back(solver.MakeSum(queens[i], -i)->Var());
  }
  solver.AddConstraint(solver.MakeAllDifferent(diag_1));
  solver.AddConstraint(solver.MakeAllDifferent(diag_2));

  DecisionBuilder* const db = solver.MakePhase(
      queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);

  // Iterates through the solutions, displaying each.
  int num_solutions = 0;

  solver.NewSearch(db);
  while (solver.NextSolution()) {
    // Displays the solution just computed.
    LOG(INFO) << "Solution " << num_solutions;
    for (int i = 0; i < board_size; ++i) {
      std::stringstream ss;
      for (int j = 0; j < board_size; ++j) {
        if (queens[j]->Value() == i) {
          // There is a queen in column j, row i.
          ss << "Q";
        } else {
          ss << "_";
        }
        if (j != board_size - 1) ss << " ";
      }
      LOG(INFO) << ss.str();
    }
    num_solutions++;
  }
  solver.EndSearch();

  // Statistics.
  LOG(INFO) << "Statistics";
  LOG(INFO) << "  failures: " << solver.failures();
  LOG(INFO) << "  branches: " << solver.branches();
  LOG(INFO) << "  wall time: " << solver.wall_time() << " ms";
  LOG(INFO) << "  Solutions found: " << num_solutions;
}

}  // namespace operations_research

int main(int argc, char** argv) {
  int board_size = 8;
  if (argc > 1) {
    board_size = std::atoi(argv[1]);
  }
  operations_research::NQueensCp(board_size);
  return EXIT_SUCCESS;
}

Java

// OR-Tools solution to the N-queens problem.
package com.google.ortools.constraintsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.constraintsolver.DecisionBuilder;
import com.google.ortools.constraintsolver.IntVar;
import com.google.ortools.constraintsolver.Solver;

/** N-Queens Problem. */
public final class NQueensCp {
  public static void main(String[] args) {
    Loader.loadNativeLibraries();
    // Instantiate the solver.
    Solver solver = new Solver("N-Queens");

    int boardSize = 8;
    IntVar[] queens = new IntVar[boardSize];
    for (int i = 0; i < boardSize; ++i) {
      queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i);
    }

    // Define constraints.
    // All rows must be different.
    solver.addConstraint(solver.makeAllDifferent(queens));

    // All columns must be different because the indices of queens are all different.
    // No two queens can be on the same diagonal.
    IntVar[] diag1 = new IntVar[boardSize];
    IntVar[] diag2 = new IntVar[boardSize];
    for (int i = 0; i < boardSize; ++i) {
      diag1[i] = solver.makeSum(queens[i], i).var();
      diag2[i] = solver.makeSum(queens[i], -i).var();
    }
    solver.addConstraint(solver.makeAllDifferent(diag1));
    solver.addConstraint(solver.makeAllDifferent(diag2));

    // Create the decision builder to search for solutions.
    final DecisionBuilder db =
        solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);

    int solutionCount = 0;
    solver.newSearch(db);
    while (solver.nextSolution()) {
      System.out.println("Solution " + solutionCount);
      for (int i = 0; i < boardSize; ++i) {
        for (int j = 0; j < boardSize; ++j) {
          if (queens[j].value() == i) {
            System.out.print("Q");
          } else {
            System.out.print("_");
          }
          if (j != boardSize - 1) {
            System.out.print(" ");
          }
        }
        System.out.println();
      }
      solutionCount++;
    }
    solver.endSearch();

    // Statistics.
    System.out.println("Statistics");
    System.out.println("  failures: " + solver.failures());
    System.out.println("  branches: " + solver.branches());
    System.out.println("  wall time: " + solver.wallTime() + "ms");
    System.out.println("  Solutions found: " + solutionCount);
  }

  private NQueensCp() {}
}

C#

// OR-Tools solution to the N-queens problem.
using System;
using Google.OrTools.ConstraintSolver;

public class NQueensCp
{
    public static void Main(String[] args)
    {
        // Instantiate the solver.
        Solver solver = new Solver("N-Queens");

        const int BoardSize = 8;
        IntVar[] queens = new IntVar[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}");
        }

        // Define constraints.
        // All rows must be different.
        solver.Add(queens.AllDifferent());

        // All columns must be different because the indices of queens are all different.
        // No two queens can be on the same diagonal.
        IntVar[] diag1 = new IntVar[BoardSize];
        IntVar[] diag2 = new IntVar[BoardSize];
        for (int i = 0; i < BoardSize; ++i)
        {
            diag1[i] = solver.MakeSum(queens[i], i).Var();
            diag2[i] = solver.MakeSum(queens[i], -i).Var();
        }

        solver.Add(diag1.AllDifferent());
        solver.Add(diag2.AllDifferent());

        // Create the decision builder to search for solutions.
        DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);

        // Iterates through the solutions, displaying each.
        int SolutionCount = 0;
        solver.NewSearch(db);
        while (solver.NextSolution())
        {
            Console.WriteLine("Solution " + SolutionCount);
            for (int i = 0; i < BoardSize; ++i)
            {
                for (int j = 0; j < BoardSize; ++j)
                {
                    if (queens[j].Value() == i)
                    {
                        Console.Write("Q");
                    }
                    else
                    {
                        Console.Write("_");
                    }
                    if (j != BoardSize - 1)
                        Console.Write(" ");
                }
                Console.WriteLine("");
            }
            SolutionCount++;
        }
        solver.EndSearch();

        // Statistics.
        Console.WriteLine("Statistics");
        Console.WriteLine($"  failures: {solver.Failures()}");
        Console.WriteLine($"  branches: {solver.Branches()}");
        Console.WriteLine($"  wall time: {solver.WallTime()} ms");
        Console.WriteLine($"  Solutions found: {SolutionCount}");
    }
}

ソリューションの数

ソリューションの数は、取締役会の規模に応じてほぼ指数関数的に増加します。

ボードサイズ	ソリューション	すべての解を見つけるまでの時間（ミリ秒）
1	1	0
2	0	0
3	0	0
4	2	0
5	10	0
6	4	0
7	40	3
8	92	9
9	352	35
10	724	95
11	2680	378
12	14200	2198
13	73712	11628
14	365596	62427
15	2279184	410701

対称性という手法では他の解の回転が 必要な計算量を削減するために使用できます。Google が あります。上記のソリューションは高速化を意図したものではなく、シンプルです。もちろん 1 つの解決策を 1 つだけ見つけることができれば 50 までのボードサイズで数ミリ秒未満です。