W kolejnych sekcjach zobaczysz, jak tworzyć ograniczenia (CP) za pomocą zadanie kombinacyjne oparte na grze w szachy. Królowa może atakować w poziomie, pionie i ukośnie. Zadaniem „n-queens” jest pytanie:
Jak można umieścić N król na szachownicę NxN, aby żadna z nich nie atakowała i rozmawiać?
Poniżej przedstawiono jedno z możliwych rozwiązań zadania N = 4.
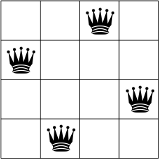
Żadne dwie królowe nie znajdują się w tym samym wierszu, kolumnie ani po przekątnej.
Nie jest to problem optymalizacji: chcemy znaleźć wszystkie możliwe zamiast jednego rozwiązania optymalnego, co sprawia, że jest on naturalnym kandydatem do programowania ograniczeń. W kolejnych sekcjach opisujemy podejście do CP do problemu N-queens. Przedstaw programy, które go rozwiązują przy użyciu rozwiązania CP-SAT i oryginalnego CP-SAT .
Podejście CP do problemu N-queen
Rozwiązanie CP polega na systematycznym wypróbowaniu wszystkich możliwe przypisania wartości do zmiennych w zadaniu, aby znaleźć i skuteczne rozwiązania. W zadaniu z 4 królami rozwiązanie zaczyna się od lewej strony i umieszcza kolejno po jednej królowej w każdej kolumnie, w lokalizacji które nie zostały zaatakowane przez żadną z wcześniejszych władców.
Propagacja i śledzenie wsteczne
Wyszukiwanie przy użyciu programowania ograniczeń składa się z 2 kluczowych elementów:
- Rozpowszechnianie – za każdym razem, gdy rozwiązanie do rozwiązania przypisze wartość do zmiennej, funkcja Ograniczenia dodają ograniczenia możliwych wartości nieprzypisanych zmiennych. Te ograniczenia uwzględniają przyszłe przypisania zmiennych. Na przykład w dzieleniu 4 królowych za każdym razem, gdy rozwiązujący umieszcza królową, nie można umieścić żadnej innej królowej w rzędzie ani po przekątnej, na której jest obecna królowa. Rozpowszechnianie może znacznie przyspieszyć wyszukiwanie przez ograniczenie wartości zmiennych, które musi badać rozwiązanie.
- Śledzenie wsteczne występuje, gdy rozwiązanie nie może przypisać wartości do następnego z powodu ograniczeń lub znajduje rozwiązanie. W obu przypadkach parametr funkcja rozwiązań powraca do poprzedniego etapu i zmienia wartość zmiennej do wartości, której jeszcze nie wypróbowano. W przykładzie z 4 królowymi oznacza przeniesienie królowej do nowego kwadratu w bieżącej kolumnie.
Następnie zobaczysz, w jaki sposób programowanie ograniczeń wykorzystuje propagację i śledzenie wsteczne rozwiązać zadanie 4 król.
Załóżmy, że Rozwiązanie rozpoczyna się od arbitralnego umieszczenia królowej w lewym górnym rogu narożnika. To pewnego rodzaju hipoteza. może się okazać, że żadne rozwiązanie w lewym górnym rogu wskazuje królowa.
Biorąc pod uwagę tę hipotezę, jakie ograniczenia możemy wprowadzić? Jednym z ograniczeń jest to, W kolumnie może być tylko jedna królowa (szary Xs poniżej), a druga nie zezwala na wyświetlanie dwóch królowych na tej samej przekątnej (czerwony znak X poniżej).
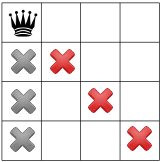
Trzecie ograniczenie zakazuje królowych z tego samego rzędu:
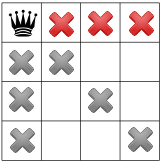
Nasze ograniczenia się rozpowszechniły, możemy przetestować kolejną hipotezę i umieścić drugą królową na jednym z pozostałych pól. Rozwiązanie może zdecydować, aby umieścić w niej pierwszy dostępny kwadrat w drugiej kolumnie:
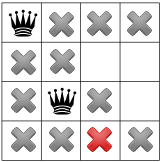
Po rozpowszechnieniu ograniczenia po przekątnej widać, że nie ma w nim dostępne kwadraty w trzeciej kolumnie lub ostatnim wierszu:
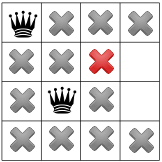
Na tym etapie nie ma żadnych rozwiązań, więc musimy cofnąć się w czasie. Jedna z opcji: aby rozwiązanie mogło wybrać inny dostępny kwadrat w drugiej kolumnie. Jednak propagacja ograniczenia powoduje, że królowa znalazła się w drugim rzędzie trzecia kolumna, pozostawiając puste miejsca dla czwartej królowej:

Rozwiązanie musi wrócić do funkcji, tym razem aż do zdarzenia pozycji pierwszej królowej. Udowodniliśmy, że nie ma rozwiązania dla królowych, będzie zajmować narożny kwadrat.
Ponieważ w rogu nie ma żadnej królowej, rozwiązanie przesuwa pierwszą królową w dół. i rozpowszechni się, zostawiając tylko jedno miejsce dla drugiej królowej:
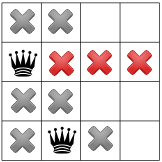
Ponowna propagacja ujawnia tylko jedno miejsce dla trzeciej królowej:
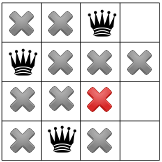
A w przypadku czwartej i ostatniej królowej:

Mamy pierwsze rozwiązanie! Jeśli poleciliśmy naszemu narzędziu, aby zatrzymał się po znalezieniu z jednego z pierwszych rozwiązań. W przeciwnym razie wróciłaby do skutku, umieścić pierwszą królową w trzecim wierszu pierwszej kolumny.
Rozwiązanie wykorzystujące CP-SAT
Problem z „n-queens” doskonale nadaje się do ograniczonego programowania. W tym omówimy krótki program w Pythonie, który używa rozwiązania CP-SAT do znaleźć wszystkie rozwiązania.
Zaimportuj biblioteki
Poniższy kod importuje wymaganą bibliotekę.
Python
import sys import time from ortools.sat.python import cp_model
C++
#include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h"
Java
import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr;
C#
using System; using Google.OrTools.Sat;
Deklarowanie modelu
Poniższy kod deklaruje model CP-SAT.
Python
model = cp_model.CpModel()
C++
CpModelBuilder cp_model;
Java
CpModel model = new CpModel();
C#
CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
Tworzenie zmiennych
Rozwiązanie do rozwiązania tworzy zmienne zadania w postaci tablicy o nazwie queens.
Python
# There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)]
C++
// There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); }
Java
int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); }
C#
int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); }
Zakładamy tutaj, że queens[j] to numer wiersza królowej w kolumnie j.
Inaczej mówiąc, queens[j] = i oznacza, że w wierszu i i kolumnie j jest królowa.
Tworzenie ograniczeń
Oto kod, który tworzy ograniczenia dla tego problemu.
Python
# All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size))
C++
// The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2);
Java
// All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2);
C#
// All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2);
Kod korzysta z metody AddAllDifferent, która wymaga wszystkich elementów
tablica zmiennej, tak aby była inna.
Zobaczmy, w jaki sposób te ograniczenia gwarantują 3 warunki monarchów N (kółka w różnych rzędach, kolumnach i na przekątnych).
Nie ma 2 królowych w tym samym wierszu
Zastosowanie metody AllDifferent rozwiązania do funkcji queens wymusza wartości funkcji
queens[j], aby były różne dla każdej wartości j, co oznacza, że wszystkie królowe muszą być
różnych wierszach.
Nie ma 2 królowych w tej samej kolumnie
To ograniczenie jest domyślnie uwzględnione w definicji elementu queens.
Ponieważ dwa elementy queens nie mogą mieć tego samego indeksu, dwie królowe nie mogą być
w tej samej kolumnie.
Nie ma dwóch królowych na tej samej przekątnej
Ograniczenie przekątnej jest trochę trudniejsze niż ograniczenia dotyczące wierszy i kolumn. Po pierwsze, jeśli dwie królowe leżą po tej samej przekątnej, jeden z następujących warunków musi mieć wartość prawda:
- Numer wiersza i numer kolumny dla każdej z dwóch królowych są takie same.
Inaczej mówiąc,
queens(j) + jma tę samą wartość dla dwóch różnych indeksów.j - Numer wiersza minus numer kolumny dla każdej z dwóch królowych jest taki sam.
W tym przypadku
queens(j) - jma tę samą wartość dla dwóch różnych indeksówj.
Jeden z tych warunków oznacza, że królowe leżą na tej samej ukośnej płaszczyźnie rosnącej ( od lewej do prawej), a drugi oznacza, że leżą na tym samym schodzie po przekątnej. Który warunek odpowiada rosnącym, a który malejącym? zależy od kolejności wierszy i kolumn. Jak wspomnieliśmy w poprzednia sekcja, kolejność nie ma wpływu na zestaw i wyglądają tak, jak je wizualizujesz.
Zatem ograniczenie po przekątnej jest takie, że wszystkie wartości queens(j) + j muszą być
różne, a wartości queens(j) - j muszą być różne, w przypadku
inny j.
Aby zastosować metodę AddAllDifferent do queens(j) + j, umieszczamy N instancji
zmiennej (j od 0 do N-1) do tablicy diag1 w następujący sposób:
q1 = model.NewIntVar(0, 2 * board_size, 'diag1_%i' % i) diag1.append(q1) model.Add(q1 == queens[j] + j)
Następnie stosujemy AddAllDifferent do: diag1.
model.AddAllDifferent(diag1)
Ograniczenie dla queens(j) - j jest tworzone w podobny sposób.
Tworzenie drukarki rozwiązań
Aby wydrukować wszystkie rozwiązania zadania N-queens, musisz przekazać wywołanie zwrotne, nazywaną drukarką rozwiązań, do rozwiązania CP-SAT. Wywołanie powoduje wydrukowanie każdego gdy znajdzie nowe rozwiązanie. Ten kod tworzy rozwiązanie drukarki.
Python
class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print()
C++
int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; }));
Java
static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; }
C#
public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; }
Pamiętaj, że drukarka rozwiązania musi być napisana jako klasa Pythona, ponieważ Interfejs Pythona do bazowego rozwiązania C++.
Rozwiązania są wydrukowane na drukarce w następujący sposób:
for v in self.__variables: print('%s = %i' % (v, self.Value(v)), end = ' ')
W tym przykładzie self.__variables to zmienna queens, a każde v
odpowiada jednemu z 8 pozycji w queens. Powoduje to wydrukowanie rozwiązania w
następujący formularz: x0 = queens(0) x1 = queens(1) ... x7 = queens(7), gdzie
xi to numer kolumny królowej w wierszu i.
W następnej sekcji znajdziesz przykładowe rozwiązanie.
Wywołaj rozwiązanie i wyświetl wyniki
Ten kod uruchamia i wyświetla rozwiązania.
Python
solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer)
C++
// Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions;
Java
CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb);
C#
// Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb);
Program znajduje 92 różne rozwiązania tablicy 8 x 8. Oto pierwsze.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Solutions found: 92Możesz rozwiązać zadanie dla tablicy o innym rozmiarze, podając N jako
wiersza poleceń. Jeśli na przykład program nazywa się queens,
python nqueens_sat.py 6 rozwiązuje problem planszy 6 x 6.
Cały program
Oto cały program programu N-queens.
Python
"""OR-Tools solution to the N-queens problem.""" import sys import time from ortools.sat.python import cp_model class NQueenSolutionPrinter(cp_model.CpSolverSolutionCallback): """Print intermediate solutions.""" def __init__(self, queens: list[cp_model.IntVar]): cp_model.CpSolverSolutionCallback.__init__(self) self.__queens = queens self.__solution_count = 0 self.__start_time = time.time() @property def solution_count(self) -> int: return self.__solution_count def on_solution_callback(self): current_time = time.time() print( f"Solution {self.__solution_count}, " f"time = {current_time - self.__start_time} s" ) self.__solution_count += 1 all_queens = range(len(self.__queens)) for i in all_queens: for j in all_queens: if self.value(self.__queens[j]) == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() def main(board_size: int) -> None: # Creates the solver. model = cp_model.CpModel() # Creates the variables. # There are `board_size` number of variables, one for a queen in each column # of the board. The value of each variable is the row that the queen is in. queens = [model.new_int_var(0, board_size - 1, f"x_{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. model.add_all_different(queens) # No two queens can be on the same diagonal. model.add_all_different(queens[i] + i for i in range(board_size)) model.add_all_different(queens[i] - i for i in range(board_size)) # Solve the model. solver = cp_model.CpSolver() solution_printer = NQueenSolutionPrinter(queens) solver.parameters.enumerate_all_solutions = True solver.solve(model, solution_printer) # Statistics. print("\nStatistics") print(f" conflicts : {solver.num_conflicts}") print(f" branches : {solver.num_branches}") print(f" wall time : {solver.wall_time} s") print(f" solutions found: {solution_printer.solution_count}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <stdlib.h> #include <sstream> #include <string> #include <vector> #include "absl/strings/numbers.h" #include "ortools/base/logging.h" #include "ortools/sat/cp_model.h" #include "ortools/sat/cp_model.pb.h" #include "ortools/sat/cp_model_solver.h" #include "ortools/sat/model.h" #include "ortools/sat/sat_parameters.pb.h" #include "ortools/util/sorted_interval_list.h" namespace operations_research { namespace sat { void NQueensSat(const int board_size) { // Instantiate the solver. CpModelBuilder cp_model; // There are `board_size` number of variables, one for a queen in each column // of the board. The value of each variable is the row that the queen is in. std::vector<IntVar> queens; queens.reserve(board_size); Domain range(0, board_size - 1); for (int i = 0; i < board_size; ++i) { queens.push_back( cp_model.NewIntVar(range).WithName("x" + std::to_string(i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. cp_model.AddAllDifferent(queens); // No two queens can be on the same diagonal. std::vector<LinearExpr> diag_1; diag_1.reserve(board_size); std::vector<LinearExpr> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(queens[i] + i); diag_2.push_back(queens[i] - i); } cp_model.AddAllDifferent(diag_1); cp_model.AddAllDifferent(diag_2); int num_solutions = 0; Model model; model.Add(NewFeasibleSolutionObserver([&](const CpSolverResponse& response) { LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (SolutionIntegerValue(response, queens[j]) == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; })); // Tell the solver to enumerate all solutions. SatParameters parameters; parameters.set_enumerate_all_solutions(true); model.Add(NewSatParameters(parameters)); const CpSolverResponse response = SolveCpModel(cp_model.Build(), &model); LOG(INFO) << "Number of solutions found: " << num_solutions; // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << CpSolverResponseStats(response); } } // namespace sat } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { if (!absl::SimpleAtoi(argv[1], &board_size)) { LOG(INFO) << "Cannot parse '" << argv[1] << "', using the default value of 8."; board_size = 8; } } operations_research::sat::NQueensSat(board_size); return EXIT_SUCCESS; }
Java
package com.google.ortools.sat.samples; import com.google.ortools.Loader; import com.google.ortools.sat.CpModel; import com.google.ortools.sat.CpSolver; import com.google.ortools.sat.CpSolverSolutionCallback; import com.google.ortools.sat.IntVar; import com.google.ortools.sat.LinearExpr; /** OR-Tools solution to the N-queens problem. */ public final class NQueensSat { static class SolutionPrinter extends CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queensIn) { solutionCount = 0; queens = queensIn; } @Override public void onSolutionCallback() { System.out.println("Solution " + solutionCount); for (int i = 0; i < queens.length; ++i) { for (int j = 0; j < queens.length; ++j) { if (value(queens[j]) == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != queens.length - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } public int getSolutionCount() { return solutionCount; } private int solutionCount; private final IntVar[] queens; } public static void main(String[] args) { Loader.loadNativeLibraries(); // Create the model. CpModel model = new CpModel(); int boardSize = 8; // There are `BoardSize` number of variables, one for a queen in each column of the board. The // value of each variable is the row that the queen is in. IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = model.newIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. model.addAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[boardSize]; LinearExpr[] diag2 = new LinearExpr[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = LinearExpr.newBuilder().add(queens[i]).add(i).build(); diag2[i] = LinearExpr.newBuilder().add(queens[i]).add(-i).build(); } model.addAllDifferent(diag1); model.addAllDifferent(diag2); // Create a solver and solve the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Tell the solver to enumerate all solutions. solver.getParameters().setEnumerateAllSolutions(true); // And solve. solver.solve(model, cb); // Statistics. System.out.println("Statistics"); System.out.println(" conflicts : " + solver.numConflicts()); System.out.println(" branches : " + solver.numBranches()); System.out.println(" wall time : " + solver.wallTime() + " s"); System.out.println(" solutions : " + cb.getSolutionCount()); } private NQueensSat() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.Sat; public class NQueensSat { public class SolutionPrinter : CpSolverSolutionCallback { public SolutionPrinter(IntVar[] queens) { queens_ = queens; } public override void OnSolutionCallback() { Console.WriteLine($"Solution {SolutionCount_}"); for (int i = 0; i < queens_.Length; ++i) { for (int j = 0; j < queens_.Length; ++j) { if (Value(queens_[j]) == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != queens_.Length - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount_++; } public int SolutionCount() { return SolutionCount_; } private int SolutionCount_; private IntVar[] queens_; } static void Main() { // Constraint programming engine CpModel model = new CpModel(); int BoardSize = 8; // There are `BoardSize` number of variables, one for a queen in each // column of the board. The value of each variable is the row that the // queen is in. IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = model.NewIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. model.AddAllDifferent(queens); // No two queens can be on the same diagonal. LinearExpr[] diag1 = new LinearExpr[BoardSize]; LinearExpr[] diag2 = new LinearExpr[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/i); diag2[i] = LinearExpr.Affine(queens[i], /*coeff=*/1, /*offset=*/-i); } model.AddAllDifferent(diag1); model.AddAllDifferent(diag2); // Creates a solver and solves the model. CpSolver solver = new CpSolver(); SolutionPrinter cb = new SolutionPrinter(queens); // Search for all solutions. solver.StringParameters = "enumerate_all_solutions:true"; // And solve. solver.Solve(model, cb); Console.WriteLine("Statistics"); Console.WriteLine($" conflicts : {solver.NumConflicts()}"); Console.WriteLine($" branches : {solver.NumBranches()}"); Console.WriteLine($" wall time : {solver.WallTime()} s"); Console.WriteLine($" number of solutions found: {cb.SolutionCount()}"); } }
Rozwiązanie używające oryginalnego rozwiązania CP
W kolejnych sekcjach przedstawiamy program w Pythonie, który rozwiązuje problemy z królami N przy użyciu oryginalnego rozwiązania CP. Zalecamy jednak korzystanie z nowszego rozwiązania CP-SAT.
Zaimportuj biblioteki
Poniższy kod importuje wymaganą bibliotekę.
Python
import sys from ortools.constraint_solver import pywrapcp
C++
#include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h"
Java
import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver;
C#
using System; using Google.OrTools.ConstraintSolver;
Zadeklarowanie rozwiązania
Ten kod deklaruje oryginalne rozwiązanie CP.
Python
solver = pywrapcp.Solver("n-queens")
C++
Solver solver("N-Queens");
Java
Solver solver = new Solver("N-Queens");
C#
Solver solver = new Solver("N-Queens");
Tworzenie zmiennych
Metoda IntVar rozwiązania tworzy zmienne dla zadania w postaci tablicy
o nazwie queens.
Python
# The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)]
C++
std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); }
Java
int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); }
C#
const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); }
W przypadku każdego rozwiązania queens[j] = i oznacza, że w kolumnie j i wierszu jest królowa
i
Tworzenie ograniczeń
Oto kod, który tworzy ograniczenia dla tego problemu.
Python
# All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)]))
C++
// The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2));
Java
// All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2));
C#
// All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent());
Te ograniczenia gwarantują 3 warunki problemu n-queens ( w różnych rzędach, kolumnach i po przekątnych).
Nie ma 2 królowych w tym samym wierszu
Zastosowanie metody AllDifferent rozwiązania do funkcji queens wymusza wartości funkcji
queens[j], aby były różne dla każdej wartości j, co oznacza, że wszystkie królowe muszą być
różnych wierszach.
Nie ma 2 królowych w tej samej kolumnie
To ograniczenie jest domyślnie uwzględnione w definicji elementu queens.
Ponieważ dwa elementy queens nie mogą mieć tego samego indeksu, dwie królowe nie mogą być
w tej samej kolumnie.
Nie ma dwóch królowych na tej samej przekątnej
Ograniczenie przekątnej jest trochę trudniejsze niż ograniczenia dotyczące wierszy i kolumn. Po pierwsze, jeśli dwie królowe leżą po tej samej przekątnej, musi być spełniony jeden z tych warunków:
- Jeśli przekątna pada malejąco (od lewej do prawej), to znak plusa
są równe.
queens(i) + ima więc tę samą wartość dla dwóch różnych indeksówi. - Jeśli przekątna jest rosnąca, numer wiersza minus numer kolumny dla każdego z nich
jest równe. W tym przypadku
queens(i) - ima tę samą wartość dla dwóch różnych indeksówi.
Zatem ograniczenie po przekątnej jest takie, że wszystkie wartości queens(i) + i muszą być
różne i analogicznie wartości queens(i) - i muszą być różne, w przypadku
inny i.
Powyższy kod dodaje to ograniczenie przez zastosowanie
AllDifferent
do queens[j] + j i queens[j] - j dla każdej metody i.
Dodaj narzędzie do podejmowania decyzji
Następnym krokiem jest utworzenie narzędzia do podejmowania decyzji, które wyznacza strategię w sieci wyszukiwania do rozwiązania problemu. Strategia wyszukiwania może mieć duży wpływ na czas wyszukiwania, ze względu na propagację ograniczeń, co zmniejsza liczbę wartości zmiennych musi znaleźć rozwiązanie. To jest już przykład na Przykład: 4 królowe.
Ten kod tworzy kreator decyzji oparty na
Phase
.
Python
db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE)
C++
DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE);
Java
// Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
C#
// Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE);
Zajrzyj na stronę Kreator decyzji, aby uzyskać szczegółowe informacje
argumentów wejściowych do metody Phase.
Jak działa narzędzie do podejmowania decyzji w przykładzie z 4 królowymi
Spójrzmy na sposób, w jaki narzędzie do podejmowania decyzji kieruje wyszukiwaniem
Przykład: 4 królowe.
Rozwiązanie zaczyna się od queens[0], pierwszej zmiennej w tablicy, zgodnie ze wskazówkami
autor: CHOOSE_FIRST_UNBOUND. Następnie rozwiązanie przypisuje do queens[0] najmniejszą wartość
, która nie została jeszcze wypróbowana, czyli wynosi 0 na tym etapie, zgodnie z instrukcją
ASSIGN_MIN_VALUE Pierwsza królowa pojawia się w lewym górnym rogu
pokład.
Następnie rozwiązanie wybiera zmienną queens[1], która jest teraz pierwszą niepowiązaną zmienną w
queens Po wprowadzeniu ograniczeń mogą pojawić się 2 wiersze:
królowa w kolumnie 1: wiersz 2 lub wiersz 3. Opcja ASSIGN_MIN_VALUE kieruje
do przypisania queens[1] = 2. (Jeśli zamiast tego ustawisz IntValueStrategy na
ASSIGN_MAX_VALUE, narzędzie do rozwiązania przypisze wartość queens[1] = 3).
Możesz sprawdzić, czy reszta wyszukiwania podlega tym samym regułom.
Wywołaj rozwiązanie i wyświetl wyniki
Ten kod uruchamia i wyświetla rozwiązanie.
Python
# Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch()
C++
// Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch();
Java
int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch();
C#
// Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch();
Oto pierwsze rozwiązanie znalezione przez program dla planszy 8 x 8.
Q _ _ _ _ _ _ _
_ _ _ _ _ _ Q _
_ _ _ _ Q _ _ _
_ _ _ _ _ _ _ Q
_ Q _ _ _ _ _ _
_ _ _ Q _ _ _ _
_ _ _ _ _ Q _ _
_ _ Q _ _ _ _ _
...91 other solutions displayed...
Statistics
failures: 304
branches: 790
wall time: 5 ms
Solutions found: 92Możesz rozwiązać zadanie dla tablicy o innym rozmiarze, podając N jako
wiersza poleceń. Na przykład funkcja python nqueens_cp.py 6 rozwiązuje problem
dla planszy 6 x 6.
Cały program
Pełny program znajdziesz poniżej.
Python
"""OR-Tools solution to the N-queens problem.""" import sys from ortools.constraint_solver import pywrapcp def main(board_size): # Creates the solver. solver = pywrapcp.Solver("n-queens") # Creates the variables. # The array index is the column, and the value is the row. queens = [solver.IntVar(0, board_size - 1, f"x{i}") for i in range(board_size)] # Creates the constraints. # All rows must be different. solver.Add(solver.AllDifferent(queens)) # No two queens can be on the same diagonal. solver.Add(solver.AllDifferent([queens[i] + i for i in range(board_size)])) solver.Add(solver.AllDifferent([queens[i] - i for i in range(board_size)])) db = solver.Phase(queens, solver.CHOOSE_FIRST_UNBOUND, solver.ASSIGN_MIN_VALUE) # Iterates through the solutions, displaying each. num_solutions = 0 solver.NewSearch(db) while solver.NextSolution(): # Displays the solution just computed. for i in range(board_size): for j in range(board_size): if queens[j].Value() == i: # There is a queen in column j, row i. print("Q", end=" ") else: print("_", end=" ") print() print() num_solutions += 1 solver.EndSearch() # Statistics. print("\nStatistics") print(f" failures: {solver.Failures()}") print(f" branches: {solver.Branches()}") print(f" wall time: {solver.WallTime()} ms") print(f" Solutions found: {num_solutions}") if __name__ == "__main__": # By default, solve the 8x8 problem. size = 8 if len(sys.argv) > 1: size = int(sys.argv[1]) main(size)
C++
// OR-Tools solution to the N-queens problem. #include <cstdint> #include <cstdlib> #include <sstream> #include <vector> #include "ortools/base/logging.h" #include "ortools/constraint_solver/constraint_solver.h" namespace operations_research { void NQueensCp(const int board_size) { // Instantiate the solver. Solver solver("N-Queens"); std::vector<IntVar*> queens; queens.reserve(board_size); for (int i = 0; i < board_size; ++i) { queens.push_back( solver.MakeIntVar(0, board_size - 1, absl::StrCat("x", i))); } // Define constraints. // The following sets the constraint that all queens are in different rows. solver.AddConstraint(solver.MakeAllDifferent(queens)); // All columns must be different because the indices of queens are all // different. No two queens can be on the same diagonal. std::vector<IntVar*> diag_1; diag_1.reserve(board_size); std::vector<IntVar*> diag_2; diag_2.reserve(board_size); for (int i = 0; i < board_size; ++i) { diag_1.push_back(solver.MakeSum(queens[i], i)->Var()); diag_2.push_back(solver.MakeSum(queens[i], -i)->Var()); } solver.AddConstraint(solver.MakeAllDifferent(diag_1)); solver.AddConstraint(solver.MakeAllDifferent(diag_2)); DecisionBuilder* const db = solver.MakePhase( queens, Solver::CHOOSE_FIRST_UNBOUND, Solver::ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int num_solutions = 0; solver.NewSearch(db); while (solver.NextSolution()) { // Displays the solution just computed. LOG(INFO) << "Solution " << num_solutions; for (int i = 0; i < board_size; ++i) { std::stringstream ss; for (int j = 0; j < board_size; ++j) { if (queens[j]->Value() == i) { // There is a queen in column j, row i. ss << "Q"; } else { ss << "_"; } if (j != board_size - 1) ss << " "; } LOG(INFO) << ss.str(); } num_solutions++; } solver.EndSearch(); // Statistics. LOG(INFO) << "Statistics"; LOG(INFO) << " failures: " << solver.failures(); LOG(INFO) << " branches: " << solver.branches(); LOG(INFO) << " wall time: " << solver.wall_time() << " ms"; LOG(INFO) << " Solutions found: " << num_solutions; } } // namespace operations_research int main(int argc, char** argv) { int board_size = 8; if (argc > 1) { board_size = std::atoi(argv[1]); } operations_research::NQueensCp(board_size); return EXIT_SUCCESS; }
Java
// OR-Tools solution to the N-queens problem. package com.google.ortools.constraintsolver.samples; import com.google.ortools.Loader; import com.google.ortools.constraintsolver.DecisionBuilder; import com.google.ortools.constraintsolver.IntVar; import com.google.ortools.constraintsolver.Solver; /** N-Queens Problem. */ public final class NQueensCp { public static void main(String[] args) { Loader.loadNativeLibraries(); // Instantiate the solver. Solver solver = new Solver("N-Queens"); int boardSize = 8; IntVar[] queens = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { queens[i] = solver.makeIntVar(0, boardSize - 1, "x" + i); } // Define constraints. // All rows must be different. solver.addConstraint(solver.makeAllDifferent(queens)); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[boardSize]; IntVar[] diag2 = new IntVar[boardSize]; for (int i = 0; i < boardSize; ++i) { diag1[i] = solver.makeSum(queens[i], i).var(); diag2[i] = solver.makeSum(queens[i], -i).var(); } solver.addConstraint(solver.makeAllDifferent(diag1)); solver.addConstraint(solver.makeAllDifferent(diag2)); // Create the decision builder to search for solutions. final DecisionBuilder db = solver.makePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); int solutionCount = 0; solver.newSearch(db); while (solver.nextSolution()) { System.out.println("Solution " + solutionCount); for (int i = 0; i < boardSize; ++i) { for (int j = 0; j < boardSize; ++j) { if (queens[j].value() == i) { System.out.print("Q"); } else { System.out.print("_"); } if (j != boardSize - 1) { System.out.print(" "); } } System.out.println(); } solutionCount++; } solver.endSearch(); // Statistics. System.out.println("Statistics"); System.out.println(" failures: " + solver.failures()); System.out.println(" branches: " + solver.branches()); System.out.println(" wall time: " + solver.wallTime() + "ms"); System.out.println(" Solutions found: " + solutionCount); } private NQueensCp() {} }
C#
// OR-Tools solution to the N-queens problem. using System; using Google.OrTools.ConstraintSolver; public class NQueensCp { public static void Main(String[] args) { // Instantiate the solver. Solver solver = new Solver("N-Queens"); const int BoardSize = 8; IntVar[] queens = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { queens[i] = solver.MakeIntVar(0, BoardSize - 1, $"x{i}"); } // Define constraints. // All rows must be different. solver.Add(queens.AllDifferent()); // All columns must be different because the indices of queens are all different. // No two queens can be on the same diagonal. IntVar[] diag1 = new IntVar[BoardSize]; IntVar[] diag2 = new IntVar[BoardSize]; for (int i = 0; i < BoardSize; ++i) { diag1[i] = solver.MakeSum(queens[i], i).Var(); diag2[i] = solver.MakeSum(queens[i], -i).Var(); } solver.Add(diag1.AllDifferent()); solver.Add(diag2.AllDifferent()); // Create the decision builder to search for solutions. DecisionBuilder db = solver.MakePhase(queens, Solver.CHOOSE_FIRST_UNBOUND, Solver.ASSIGN_MIN_VALUE); // Iterates through the solutions, displaying each. int SolutionCount = 0; solver.NewSearch(db); while (solver.NextSolution()) { Console.WriteLine("Solution " + SolutionCount); for (int i = 0; i < BoardSize; ++i) { for (int j = 0; j < BoardSize; ++j) { if (queens[j].Value() == i) { Console.Write("Q"); } else { Console.Write("_"); } if (j != BoardSize - 1) Console.Write(" "); } Console.WriteLine(""); } SolutionCount++; } solver.EndSearch(); // Statistics. Console.WriteLine("Statistics"); Console.WriteLine($" failures: {solver.Failures()}"); Console.WriteLine($" branches: {solver.Branches()}"); Console.WriteLine($" wall time: {solver.WallTime()} ms"); Console.WriteLine($" Solutions found: {SolutionCount}"); } }
Liczba rozwiązań
Liczba rozwiązań zwiększa się mniej więcej wykładniczo wraz z rozmiarem tablicy:
| Rozmiar planszy | Rozwiązania | Czas znalezienia wszystkich rozwiązań (ms) |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 2 | 0 |
| 5 | 10 | 0 |
| 6 | 4 | 0 |
| 7 | 40 | 3 |
| 8 | 92 | 9 |
| 9 | 352 | 35 |
| 10 | 724 | 95 |
| 11 | 2680 | 378 |
| 12 | 14200 | 2198 |
| 13 | 73712 | 11628 |
| 14 | 365596 | 62427 |
| 15 | 2279184 | 410701 |
Wiele rozwiązań stanowi po prostu obroty innych i technikę zwaną symetrią. złamania można wykorzystać do zmniejszenia ilości potrzebnej obliczeń. Nie wykorzystujemy który tutaj; nasze rozwiązanie nie jest szybkie, tylko proste. Oczywiście. Moglibyśmy przyspieszyć cały proces, gdybyśmy chcieli znaleźć tylko jedno rozwiązanie zamiast wszystkie: nie więcej niż kilka milisekund dla plansz o rozmiarze do 50.
