इस पेज का अनुवाद Cloud Translation API से किया गया है.

एलपी की समस्या को हल करना

नीचे दिए गए सेक्शन में एलपी के सवाल का एक उदाहरण दिया गया है. इसमें बताया गया है कि इसे कैसे हल किया जा सकता है. यह समस्या इस तरह है:

3x + 4y को इन शर्तों के आधार पर बढ़ाएं:

x + 2y ≤ 14
3x - y ≥ 0
x - y ≤ 2

मकसद फ़ंक्शन, 3x + 4y, और कंस्ट्रेंट, दोनों लीनियर एक्सप्रेशन की मदद से तय किए जाते हैं, जिससे यह एक लीनियर सवाल बन जाता है.

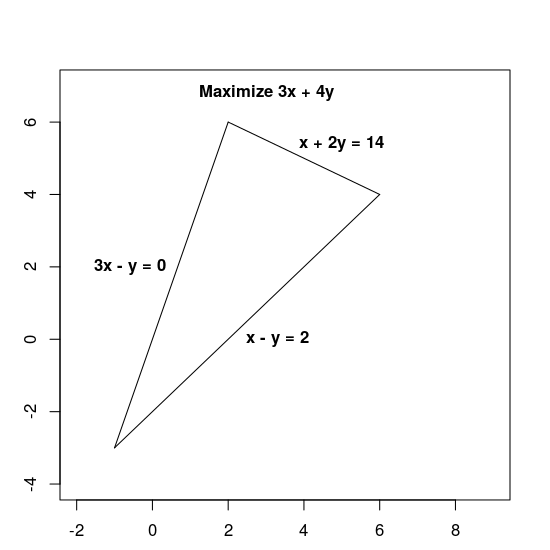
कंस्ट्रेंट से, सही इलाके के बारे में पता चलता है. यही वह त्रिभुज है जिसे नीचे दिखाया गया है. साथ ही, इसमें अंदरूनी हिस्से भी शामिल हैं.

एलपी समस्या को हल करने के बुनियादी तरीके

एलपी की समस्या को हल करने के लिए, आपके प्रोग्राम में ये तरीके शामिल होने चाहिए:

लीनियर सॉल्वर रैपर इंपोर्ट करें.
मुझे एलपी सॉल्वर का एलान करना चाहिए.
और वैरिएबल तय करें,
उन सीमाओं को तय करते हैं,
और हमारे प्रॉडक्ट का मकसद
एलपी सॉल्वर को कॉल करो; और
समाधान दिखाएं

एमपीसॉल्वर की मदद से समाधान पाना

इस सेक्शन में एक ऐसा प्रोग्राम दिया गया है जो MPSolver रैपर और एलपी सॉल्वर की मदद से सवाल को हल करता है.

ध्यान दें. नीचे दिए गए प्रोग्राम को चलाने के लिए, आपको OR-टूल इंस्टॉल करना होगा.

प्राइमरी OR-टूल लीनियर ऑप्टिमाइज़ेशन सॉल्वर Glop है. यह Google का इन-हाउस लीनियर प्रोग्रामिंग सॉल्वर है. यह तेज़, मेमोरी की क्षमता बढ़ाने वाला, और अंकों के हिसाब से स्थिर है.

लीनियर सॉल्वर रैपर इंपोर्ट करना

OR-टूल लीनियर सॉल्वर रैपर, इंपोर्ट (या शामिल करें) करें. यह एमआईपी सॉल्वर और लीनियर सॉल्वर के लिए एक इंटरफ़ेस है, जैसा कि यहां दिखाया गया है.

Python

from ortools.linear_solver import pywraplp

C++

#include <iostream>
#include <memory>

#include "ortools/linear_solver/linear_solver.h"

Java

import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;

C#

using System;
using Google.OrTools.LinearSolver;

एलपी सॉल्वर का एलान करना

MPsolver, कई अलग-अलग सॉल्वर के लिए रैपर है. इनमें ग्लोप भी शामिल है. नीचे दिया गया कोड, GLOP सॉल्वर का एलान करता है.

Python

solver = pywraplp.Solver.CreateSolver("GLOP")
if not solver:
    return

C++

std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
if (!solver) {
  LOG(WARNING) << "SCIP solver unavailable.";
  return;
}

Java

MPSolver solver = MPSolver.createSolver("GLOP");

C#

Solver solver = Solver.CreateSolver("GLOP");
if (solver is null)
{
    return;
}

ध्यान दें: किसी अन्य एलपी सॉल्वर का इस्तेमाल करने के लिए, GLOP की जगह PDLP की जगह चुनें. सॉल्वर चुनने के बारे में ज़्यादा जानने के लिए, एलपी के बेहतर समाधान देखें. साथ ही, थर्ड पार्टी सॉल्वर इंस्टॉल करने के बारे में जानने के लिए, इंस्टॉलेशन गाइड देखें.

वैरिएबल बनाना

सबसे पहले, x और y वैरिएबल बनाएं, जिनकी वैल्यू 0 से लेकर अनगिनत तक की रेंज में है.

Python

x = solver.NumVar(0, solver.infinity(), "x")
y = solver.NumVar(0, solver.infinity(), "y")

print("Number of variables =", solver.NumVariables())

C++

const double infinity = solver->infinity();
// x and y are non-negative variables.
MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x");
MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y");
LOG(INFO) << "Number of variables = " << solver->NumVariables();

Java

double infinity = java.lang.Double.POSITIVE_INFINITY;
// x and y are continuous non-negative variables.
MPVariable x = solver.makeNumVar(0.0, infinity, "x");
MPVariable y = solver.makeNumVar(0.0, infinity, "y");
System.out.println("Number of variables = " + solver.numVariables());

C#

Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x");
Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y");

Console.WriteLine("Number of variables = " + solver.NumVariables());

सीमा तय करना

इसके बाद, वैरिएबल की सीमाएं तय करें. हर कंस्ट्रेंट को एक यूनीक नाम (जैसे कि constraint0) दें. इसके बाद, कंस्ट्रेंट के लिए गुणांक तय करें.

Python

# Constraint 0: x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0)

# Constraint 1: 3x - y >= 0.
solver.Add(3 * x - y >= 0.0)

# Constraint 2: x - y <= 2.
solver.Add(x - y <= 2.0)

print("Number of constraints =", solver.NumConstraints())

C++

// x + 2*y <= 14.
MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 14.0);
c0->SetCoefficient(x, 1);
c0->SetCoefficient(y, 2);

// 3*x - y >= 0.
MPConstraint* const c1 = solver->MakeRowConstraint(0.0, infinity);
c1->SetCoefficient(x, 3);
c1->SetCoefficient(y, -1);

// x - y <= 2.
MPConstraint* const c2 = solver->MakeRowConstraint(-infinity, 2.0);
c2->SetCoefficient(x, 1);
c2->SetCoefficient(y, -1);
LOG(INFO) << "Number of constraints = " << solver->NumConstraints();

Java

// x + 2*y <= 14.
MPConstraint c0 = solver.makeConstraint(-infinity, 14.0, "c0");
c0.setCoefficient(x, 1);
c0.setCoefficient(y, 2);

// 3*x - y >= 0.
MPConstraint c1 = solver.makeConstraint(0.0, infinity, "c1");
c1.setCoefficient(x, 3);
c1.setCoefficient(y, -1);

// x - y <= 2.
MPConstraint c2 = solver.makeConstraint(-infinity, 2.0, "c2");
c2.setCoefficient(x, 1);
c2.setCoefficient(y, -1);
System.out.println("Number of constraints = " + solver.numConstraints());

C#

// x + 2y <= 14.
solver.Add(x + 2 * y <= 14.0);

// 3x - y >= 0.
solver.Add(3 * x - y >= 0.0);

// x - y <= 2.
solver.Add(x - y <= 2.0);

Console.WriteLine("Number of constraints = " + solver.NumConstraints());

मकसद फ़ंक्शन तय करना

नीचे दिया गया कोड, मकसद फ़ंक्शन 3x + 4y के बारे में बताता है और बताता है कि यह सबसे बड़ी समस्या है.

Python

# Objective function: 3x + 4y.
solver.Maximize(3 * x + 4 * y)

C++

// Objective function: 3x + 4y.
MPObjective* const objective = solver->MutableObjective();
objective->SetCoefficient(x, 3);
objective->SetCoefficient(y, 4);
objective->SetMaximization();

Java

// Maximize 3 * x + 4 * y.
MPObjective objective = solver.objective();
objective.setCoefficient(x, 3);
objective.setCoefficient(y, 4);
objective.setMaximization();

C#

// Objective function: 3x + 4y.
solver.Maximize(3 * x + 4 * y);

सॉल्वर को शुरू करें

यह कोड, सॉल्वर को शुरू करता है.

Python

print(f"Solving with {solver.SolverVersion()}")
status = solver.Solve()

C++

const MPSolver::ResultStatus result_status = solver->Solve();
// Check that the problem has an optimal solution.
if (result_status != MPSolver::OPTIMAL) {
  LOG(FATAL) << "The problem does not have an optimal solution!";
}

Java

final MPSolver.ResultStatus resultStatus = solver.solve();

C#

Solver.ResultStatus resultStatus = solver.Solve();

समाधान दिखाएं

यह कोड दिखाता है कि सलूशन क्या है.

Python

if status == pywraplp.Solver.OPTIMAL:
    print("Solution:")
    print(f"Objective value = {solver.Objective().Value():0.1f}")
    print(f"x = {x.solution_value():0.1f}")
    print(f"y = {y.solution_value():0.1f}")
else:
    print("The problem does not have an optimal solution.")

C++

LOG(INFO) << "Solution:";
LOG(INFO) << "Optimal objective value = " << objective->Value();
LOG(INFO) << x->name() << " = " << x->solution_value();
LOG(INFO) << y->name() << " = " << y->solution_value();

Java

if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
  System.out.println("Solution:");
  System.out.println("Objective value = " + objective.value());
  System.out.println("x = " + x.solutionValue());
  System.out.println("y = " + y.solutionValue());
} else {
  System.err.println("The problem does not have an optimal solution!");
}

C#

// Check that the problem has an optimal solution.
if (resultStatus != Solver.ResultStatus.OPTIMAL)
{
    Console.WriteLine("The problem does not have an optimal solution!");
    return;
}
Console.WriteLine("Solution:");
Console.WriteLine("Objective value = " + solver.Objective().Value());
Console.WriteLine("x = " + x.SolutionValue());
Console.WriteLine("y = " + y.SolutionValue());

सभी प्रोग्राम

सभी प्रोग्राम नीचे दिखाए गए हैं.

Python

from ortools.linear_solver import pywraplp


def LinearProgrammingExample():
    """Linear programming sample."""
    # Instantiate a Glop solver, naming it LinearExample.
    solver = pywraplp.Solver.CreateSolver("GLOP")
    if not solver:
        return

    # Create the two variables and let them take on any non-negative value.
    x = solver.NumVar(0, solver.infinity(), "x")
    y = solver.NumVar(0, solver.infinity(), "y")

    print("Number of variables =", solver.NumVariables())

    # Constraint 0: x + 2y <= 14.
    solver.Add(x + 2 * y <= 14.0)

    # Constraint 1: 3x - y >= 0.
    solver.Add(3 * x - y >= 0.0)

    # Constraint 2: x - y <= 2.
    solver.Add(x - y <= 2.0)

    print("Number of constraints =", solver.NumConstraints())

    # Objective function: 3x + 4y.
    solver.Maximize(3 * x + 4 * y)

    # Solve the system.
    print(f"Solving with {solver.SolverVersion()}")
    status = solver.Solve()

    if status == pywraplp.Solver.OPTIMAL:
        print("Solution:")
        print(f"Objective value = {solver.Objective().Value():0.1f}")
        print(f"x = {x.solution_value():0.1f}")
        print(f"y = {y.solution_value():0.1f}")
    else:
        print("The problem does not have an optimal solution.")

    print("\nAdvanced usage:")
    print(f"Problem solved in {solver.wall_time():d} milliseconds")
    print(f"Problem solved in {solver.iterations():d} iterations")


LinearProgrammingExample()

C++

#include <iostream>
#include <memory>

#include "ortools/linear_solver/linear_solver.h"

namespace operations_research {
void LinearProgrammingExample() {
  std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
  if (!solver) {
    LOG(WARNING) << "SCIP solver unavailable.";
    return;
  }

  const double infinity = solver->infinity();
  // x and y are non-negative variables.
  MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x");
  MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y");
  LOG(INFO) << "Number of variables = " << solver->NumVariables();

  // x + 2*y <= 14.
  MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 14.0);
  c0->SetCoefficient(x, 1);
  c0->SetCoefficient(y, 2);

  // 3*x - y >= 0.
  MPConstraint* const c1 = solver->MakeRowConstraint(0.0, infinity);
  c1->SetCoefficient(x, 3);
  c1->SetCoefficient(y, -1);

  // x - y <= 2.
  MPConstraint* const c2 = solver->MakeRowConstraint(-infinity, 2.0);
  c2->SetCoefficient(x, 1);
  c2->SetCoefficient(y, -1);
  LOG(INFO) << "Number of constraints = " << solver->NumConstraints();

  // Objective function: 3x + 4y.
  MPObjective* const objective = solver->MutableObjective();
  objective->SetCoefficient(x, 3);
  objective->SetCoefficient(y, 4);
  objective->SetMaximization();

  const MPSolver::ResultStatus result_status = solver->Solve();
  // Check that the problem has an optimal solution.
  if (result_status != MPSolver::OPTIMAL) {
    LOG(FATAL) << "The problem does not have an optimal solution!";
  }

  LOG(INFO) << "Solution:";
  LOG(INFO) << "Optimal objective value = " << objective->Value();
  LOG(INFO) << x->name() << " = " << x->solution_value();
  LOG(INFO) << y->name() << " = " << y->solution_value();
}
}  // namespace operations_research

int main(int argc, char** argv) {
  operations_research::LinearProgrammingExample();
  return EXIT_SUCCESS;
}

Java

package com.google.ortools.linearsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;

/** Simple linear programming example. */
public final class LinearProgrammingExample {
  public static void main(String[] args) {
    Loader.loadNativeLibraries();
    MPSolver solver = MPSolver.createSolver("GLOP");

    double infinity = java.lang.Double.POSITIVE_INFINITY;
    // x and y are continuous non-negative variables.
    MPVariable x = solver.makeNumVar(0.0, infinity, "x");
    MPVariable y = solver.makeNumVar(0.0, infinity, "y");
    System.out.println("Number of variables = " + solver.numVariables());

    // x + 2*y <= 14.
    MPConstraint c0 = solver.makeConstraint(-infinity, 14.0, "c0");
    c0.setCoefficient(x, 1);
    c0.setCoefficient(y, 2);

    // 3*x - y >= 0.
    MPConstraint c1 = solver.makeConstraint(0.0, infinity, "c1");
    c1.setCoefficient(x, 3);
    c1.setCoefficient(y, -1);

    // x - y <= 2.
    MPConstraint c2 = solver.makeConstraint(-infinity, 2.0, "c2");
    c2.setCoefficient(x, 1);
    c2.setCoefficient(y, -1);
    System.out.println("Number of constraints = " + solver.numConstraints());

    // Maximize 3 * x + 4 * y.
    MPObjective objective = solver.objective();
    objective.setCoefficient(x, 3);
    objective.setCoefficient(y, 4);
    objective.setMaximization();

    final MPSolver.ResultStatus resultStatus = solver.solve();

    if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
      System.out.println("Solution:");
      System.out.println("Objective value = " + objective.value());
      System.out.println("x = " + x.solutionValue());
      System.out.println("y = " + y.solutionValue());
    } else {
      System.err.println("The problem does not have an optimal solution!");
    }

    System.out.println("\nAdvanced usage:");
    System.out.println("Problem solved in " + solver.wallTime() + " milliseconds");
    System.out.println("Problem solved in " + solver.iterations() + " iterations");
  }

  private LinearProgrammingExample() {}
}

C#

using System;
using Google.OrTools.LinearSolver;

public class LinearProgrammingExample
{
    static void Main()
    {
        Solver solver = Solver.CreateSolver("GLOP");
        if (solver is null)
        {
            return;
        }
        // x and y are continuous non-negative variables.
        Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x");
        Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y");

        Console.WriteLine("Number of variables = " + solver.NumVariables());

        // x + 2y <= 14.
        solver.Add(x + 2 * y <= 14.0);

        // 3x - y >= 0.
        solver.Add(3 * x - y >= 0.0);

        // x - y <= 2.
        solver.Add(x - y <= 2.0);

        Console.WriteLine("Number of constraints = " + solver.NumConstraints());

        // Objective function: 3x + 4y.
        solver.Maximize(3 * x + 4 * y);

        Solver.ResultStatus resultStatus = solver.Solve();

        // Check that the problem has an optimal solution.
        if (resultStatus != Solver.ResultStatus.OPTIMAL)
        {
            Console.WriteLine("The problem does not have an optimal solution!");
            return;
        }
        Console.WriteLine("Solution:");
        Console.WriteLine("Objective value = " + solver.Objective().Value());
        Console.WriteLine("x = " + x.SolutionValue());
        Console.WriteLine("y = " + y.SolutionValue());

        Console.WriteLine("\nAdvanced usage:");
        Console.WriteLine("Problem solved in " + solver.WallTime() + " milliseconds");
        Console.WriteLine("Problem solved in " + solver.Iterations() + " iterations");
    }
}

सबसे अच्छा समाधान

प्रोग्राम समस्या का इष्टतम समाधान देता है, जैसा कि नीचे दिखाया गया है.

Number of variables = 2
Number of constraints = 3
Solution:
x = 6.0
y = 4.0
Optimal objective value = 34.0

हल दिखाने वाला एक ग्राफ़ यहां दिया गया है:

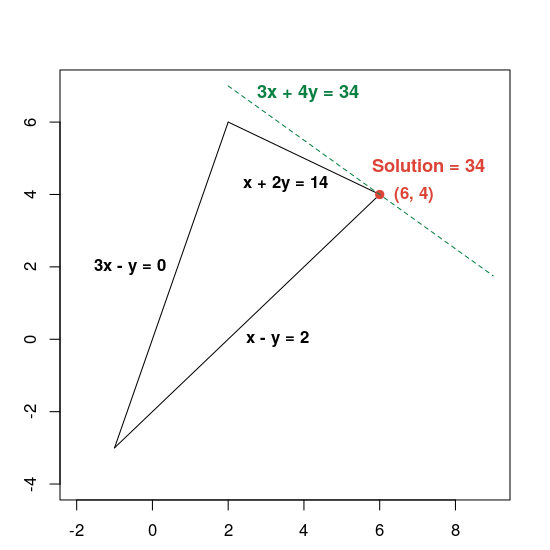
डैश वाली हरी लाइन, मकसद फ़ंक्शन को उसके इष्टतम मान 34 के बराबर सेट करके तय की जाती है. अगर किसी लाइन का समीकरण 3x + 4y = c है, तो यह डैश वाली लाइन के समान होता है. साथ ही, 34, c की सबसे बड़ी वैल्यू होती है, जिसके लिए यह लाइन सही इलाके को काटती है.

लीनियर ऑप्टिमाइज़ेशन से जुड़ी समस्याओं को हल करने के बारे में ज़्यादा जानने के लिए, एलपी को बेहतर तरीके से हल करना देखें.