В следующих разделах представлен пример проблемы MIP и показано, как ее решить. Вот проблема:
Максимизируйте x + 10y при следующих ограничениях:
-
x + 7y≤ 17,5 - 0 ≤
x≤ 3,5 - 0 ≤
y -
x,yцелые числа
Поскольку ограничения линейны, это просто задача линейной оптимизации, в которой решения должны быть целыми числами. На графике ниже показаны целочисленные точки в допустимой области задачи.
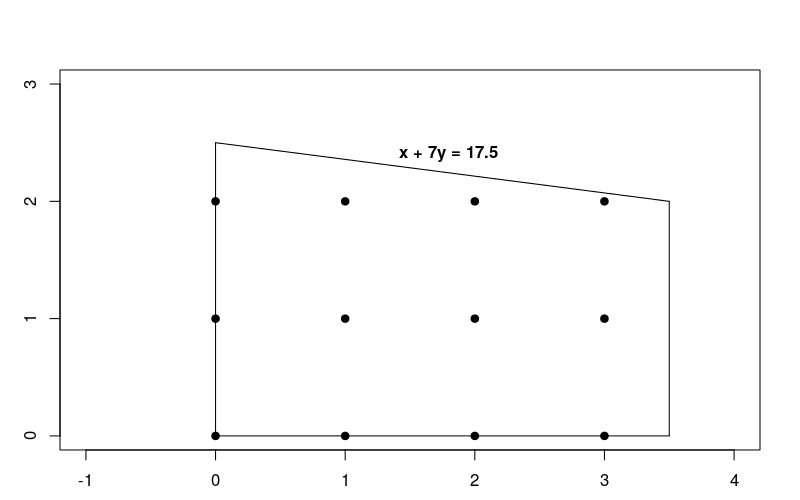
Обратите внимание, что эта проблема очень похожа на задачу линейной оптимизации, описанную в разделе «Решение задачи ЛП» , но в этом случае мы требуем, чтобы решения были целыми числами.
Основные шаги решения проблемы MIP
Чтобы решить проблему MIP, ваша программа должна включать следующие шаги:
- Импортируйте оболочку линейного решателя,
- объявить решатель MIP,
- определить переменные,
- определить ограничения,
- определить цель,
- вызвать решатель MIP и
- покажи решение
Решение с помощью MPsolver
В следующем разделе представлена программа, которая решает проблему с помощью оболочки MPsolver и решателя MIP.
MIP-решатель OR-Tools по умолчанию — SCIP .
Импортируйте оболочку линейного решателя
Импортируйте (или включите) оболочку линейного решателя OR-Tools, интерфейс для решателей MIP и линейных решателей, как показано ниже.
Питон
from ortools.linear_solver import pywraplp
С++
#include <memory> #include "ortools/linear_solver/linear_solver.h"
Джава
import com.google.ortools.Loader; import com.google.ortools.linearsolver.MPConstraint; import com.google.ortools.linearsolver.MPObjective; import com.google.ortools.linearsolver.MPSolver; import com.google.ortools.linearsolver.MPVariable;
С#
using System; using Google.OrTools.LinearSolver;
Объявить решатель MIP
Следующий код объявляет решатель MIP для этой проблемы. В этом примере используется сторонний решатель SCIP .
Питон
# Create the mip solver with the SCIP backend.
solver = pywraplp.Solver.CreateSolver("SAT")
if not solver:
returnС++
// Create the mip solver with the SCIP backend.
std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
if (!solver) {
LOG(WARNING) << "SCIP solver unavailable.";
return;
}Джава
// Create the linear solver with the SCIP backend.
MPSolver solver = MPSolver.createSolver("SCIP");
if (solver == null) {
System.out.println("Could not create solver SCIP");
return;
}С#
// Create the linear solver with the SCIP backend.
Solver solver = Solver.CreateSolver("SCIP");
if (solver is null)
{
return;
}Определите переменные
Следующий код определяет переменные в задаче.
Питон
infinity = solver.infinity()
# x and y are integer non-negative variables.
x = solver.IntVar(0.0, infinity, "x")
y = solver.IntVar(0.0, infinity, "y")
print("Number of variables =", solver.NumVariables())С++
const double infinity = solver->infinity(); // x and y are integer non-negative variables. MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x"); MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y"); LOG(INFO) << "Number of variables = " << solver->NumVariables();
Джава
double infinity = java.lang.Double.POSITIVE_INFINITY;
// x and y are integer non-negative variables.
MPVariable x = solver.makeIntVar(0.0, infinity, "x");
MPVariable y = solver.makeIntVar(0.0, infinity, "y");
System.out.println("Number of variables = " + solver.numVariables());С#
// x and y are integer non-negative variables.
Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x");
Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y");
Console.WriteLine("Number of variables = " + solver.NumVariables()); Программа использует метод MakeIntVar (или его вариант, в зависимости от языка программирования) для создания переменных x и y , которые принимают неотрицательные целочисленные значения.
Определите ограничения
Следующий код определяет ограничения для проблемы.
Питон
# x + 7 * y <= 17.5.
solver.Add(x + 7 * y <= 17.5)
# x <= 3.5.
solver.Add(x <= 3.5)
print("Number of constraints =", solver.NumConstraints())С++
// x + 7 * y <= 17.5. MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 17.5, "c0"); c0->SetCoefficient(x, 1); c0->SetCoefficient(y, 7); // x <= 3.5. MPConstraint* const c1 = solver->MakeRowConstraint(-infinity, 3.5, "c1"); c1->SetCoefficient(x, 1); c1->SetCoefficient(y, 0); LOG(INFO) << "Number of constraints = " << solver->NumConstraints();
Джава
// x + 7 * y <= 17.5.
MPConstraint c0 = solver.makeConstraint(-infinity, 17.5, "c0");
c0.setCoefficient(x, 1);
c0.setCoefficient(y, 7);
// x <= 3.5.
MPConstraint c1 = solver.makeConstraint(-infinity, 3.5, "c1");
c1.setCoefficient(x, 1);
c1.setCoefficient(y, 0);
System.out.println("Number of constraints = " + solver.numConstraints());С#
// x + 7 * y <= 17.5.
solver.Add(x + 7 * y <= 17.5);
// x <= 3.5.
solver.Add(x <= 3.5);
Console.WriteLine("Number of constraints = " + solver.NumConstraints());Определите цель
Следующий код определяет objective function для задачи.
Питон
# Maximize x + 10 * y. solver.Maximize(x + 10 * y)
С++
// Maximize x + 10 * y. MPObjective* const objective = solver->MutableObjective(); objective->SetCoefficient(x, 1); objective->SetCoefficient(y, 10); objective->SetMaximization();
Джава
// Maximize x + 10 * y. MPObjective objective = solver.objective(); objective.setCoefficient(x, 1); objective.setCoefficient(y, 10); objective.setMaximization();
С#
// Maximize x + 10 * y. solver.Maximize(x + 10 * y);
Вызов решателя
Следующий код вызывает решатель.
Питон
print(f"Solving with {solver.SolverVersion()}")
status = solver.Solve()С++
const MPSolver::ResultStatus result_status = solver->Solve();
// Check that the problem has an optimal solution.
if (result_status != MPSolver::OPTIMAL) {
LOG(FATAL) << "The problem does not have an optimal solution!";
}Джава
final MPSolver.ResultStatus resultStatus = solver.solve();
С#
Solver.ResultStatus resultStatus = solver.Solve();
Показать решение
Следующий код отображает решение.
Питон
if status == pywraplp.Solver.OPTIMAL:
print("Solution:")
print("Objective value =", solver.Objective().Value())
print("x =", x.solution_value())
print("y =", y.solution_value())
else:
print("The problem does not have an optimal solution.")С++
LOG(INFO) << "Solution:"; LOG(INFO) << "Objective value = " << objective->Value(); LOG(INFO) << "x = " << x->solution_value(); LOG(INFO) << "y = " << y->solution_value();
Джава
if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
System.out.println("Solution:");
System.out.println("Objective value = " + objective.value());
System.out.println("x = " + x.solutionValue());
System.out.println("y = " + y.solutionValue());
} else {
System.err.println("The problem does not have an optimal solution!");
}С#
// Check that the problem has an optimal solution.
if (resultStatus != Solver.ResultStatus.OPTIMAL)
{
Console.WriteLine("The problem does not have an optimal solution!");
return;
}
Console.WriteLine("Solution:");
Console.WriteLine("Objective value = " + solver.Objective().Value());
Console.WriteLine("x = " + x.SolutionValue());
Console.WriteLine("y = " + y.SolutionValue());Вот решение проблемы.
Number of variables = 2 Number of constraints = 2 Solution: Objective value = 23 x = 3 y = 2
Оптимальное значение целевой функции — 23, которое встречается в точке x = 3 , y = 2 .
Полные программы
Вот полные программы.
Питон
from ortools.linear_solver import pywraplp
def main():
# Create the mip solver with the SCIP backend.
solver = pywraplp.Solver.CreateSolver("SAT")
if not solver:
return
infinity = solver.infinity()
# x and y are integer non-negative variables.
x = solver.IntVar(0.0, infinity, "x")
y = solver.IntVar(0.0, infinity, "y")
print("Number of variables =", solver.NumVariables())
# x + 7 * y <= 17.5.
solver.Add(x + 7 * y <= 17.5)
# x <= 3.5.
solver.Add(x <= 3.5)
print("Number of constraints =", solver.NumConstraints())
# Maximize x + 10 * y.
solver.Maximize(x + 10 * y)
print(f"Solving with {solver.SolverVersion()}")
status = solver.Solve()
if status == pywraplp.Solver.OPTIMAL:
print("Solution:")
print("Objective value =", solver.Objective().Value())
print("x =", x.solution_value())
print("y =", y.solution_value())
else:
print("The problem does not have an optimal solution.")
print("\nAdvanced usage:")
print(f"Problem solved in {solver.wall_time():d} milliseconds")
print(f"Problem solved in {solver.iterations():d} iterations")
print(f"Problem solved in {solver.nodes():d} branch-and-bound nodes")
if __name__ == "__main__":
main()С++
#include <memory>
#include "ortools/linear_solver/linear_solver.h"
namespace operations_research {
void SimpleMipProgram() {
// Create the mip solver with the SCIP backend.
std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP"));
if (!solver) {
LOG(WARNING) << "SCIP solver unavailable.";
return;
}
const double infinity = solver->infinity();
// x and y are integer non-negative variables.
MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x");
MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y");
LOG(INFO) << "Number of variables = " << solver->NumVariables();
// x + 7 * y <= 17.5.
MPConstraint* const c0 = solver->MakeRowConstraint(-infinity, 17.5, "c0");
c0->SetCoefficient(x, 1);
c0->SetCoefficient(y, 7);
// x <= 3.5.
MPConstraint* const c1 = solver->MakeRowConstraint(-infinity, 3.5, "c1");
c1->SetCoefficient(x, 1);
c1->SetCoefficient(y, 0);
LOG(INFO) << "Number of constraints = " << solver->NumConstraints();
// Maximize x + 10 * y.
MPObjective* const objective = solver->MutableObjective();
objective->SetCoefficient(x, 1);
objective->SetCoefficient(y, 10);
objective->SetMaximization();
const MPSolver::ResultStatus result_status = solver->Solve();
// Check that the problem has an optimal solution.
if (result_status != MPSolver::OPTIMAL) {
LOG(FATAL) << "The problem does not have an optimal solution!";
}
LOG(INFO) << "Solution:";
LOG(INFO) << "Objective value = " << objective->Value();
LOG(INFO) << "x = " << x->solution_value();
LOG(INFO) << "y = " << y->solution_value();
LOG(INFO) << "\nAdvanced usage:";
LOG(INFO) << "Problem solved in " << solver->wall_time() << " milliseconds";
LOG(INFO) << "Problem solved in " << solver->iterations() << " iterations";
LOG(INFO) << "Problem solved in " << solver->nodes()
<< " branch-and-bound nodes";
}
} // namespace operations_research
int main(int argc, char** argv) {
operations_research::SimpleMipProgram();
return EXIT_SUCCESS;
}Джава
package com.google.ortools.linearsolver.samples;
import com.google.ortools.Loader;
import com.google.ortools.linearsolver.MPConstraint;
import com.google.ortools.linearsolver.MPObjective;
import com.google.ortools.linearsolver.MPSolver;
import com.google.ortools.linearsolver.MPVariable;
/** Minimal Mixed Integer Programming example to showcase calling the solver. */
public final class SimpleMipProgram {
public static void main(String[] args) {
Loader.loadNativeLibraries();
// Create the linear solver with the SCIP backend.
MPSolver solver = MPSolver.createSolver("SCIP");
if (solver == null) {
System.out.println("Could not create solver SCIP");
return;
}
double infinity = java.lang.Double.POSITIVE_INFINITY;
// x and y are integer non-negative variables.
MPVariable x = solver.makeIntVar(0.0, infinity, "x");
MPVariable y = solver.makeIntVar(0.0, infinity, "y");
System.out.println("Number of variables = " + solver.numVariables());
// x + 7 * y <= 17.5.
MPConstraint c0 = solver.makeConstraint(-infinity, 17.5, "c0");
c0.setCoefficient(x, 1);
c0.setCoefficient(y, 7);
// x <= 3.5.
MPConstraint c1 = solver.makeConstraint(-infinity, 3.5, "c1");
c1.setCoefficient(x, 1);
c1.setCoefficient(y, 0);
System.out.println("Number of constraints = " + solver.numConstraints());
// Maximize x + 10 * y.
MPObjective objective = solver.objective();
objective.setCoefficient(x, 1);
objective.setCoefficient(y, 10);
objective.setMaximization();
final MPSolver.ResultStatus resultStatus = solver.solve();
if (resultStatus == MPSolver.ResultStatus.OPTIMAL) {
System.out.println("Solution:");
System.out.println("Objective value = " + objective.value());
System.out.println("x = " + x.solutionValue());
System.out.println("y = " + y.solutionValue());
} else {
System.err.println("The problem does not have an optimal solution!");
}
System.out.println("\nAdvanced usage:");
System.out.println("Problem solved in " + solver.wallTime() + " milliseconds");
System.out.println("Problem solved in " + solver.iterations() + " iterations");
System.out.println("Problem solved in " + solver.nodes() + " branch-and-bound nodes");
}
private SimpleMipProgram() {}
}С#
using System;
using Google.OrTools.LinearSolver;
public class SimpleMipProgram
{
static void Main()
{
// Create the linear solver with the SCIP backend.
Solver solver = Solver.CreateSolver("SCIP");
if (solver is null)
{
return;
}
// x and y are integer non-negative variables.
Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x");
Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y");
Console.WriteLine("Number of variables = " + solver.NumVariables());
// x + 7 * y <= 17.5.
solver.Add(x + 7 * y <= 17.5);
// x <= 3.5.
solver.Add(x <= 3.5);
Console.WriteLine("Number of constraints = " + solver.NumConstraints());
// Maximize x + 10 * y.
solver.Maximize(x + 10 * y);
Solver.ResultStatus resultStatus = solver.Solve();
// Check that the problem has an optimal solution.
if (resultStatus != Solver.ResultStatus.OPTIMAL)
{
Console.WriteLine("The problem does not have an optimal solution!");
return;
}
Console.WriteLine("Solution:");
Console.WriteLine("Objective value = " + solver.Objective().Value());
Console.WriteLine("x = " + x.SolutionValue());
Console.WriteLine("y = " + y.SolutionValue());
Console.WriteLine("\nAdvanced usage:");
Console.WriteLine("Problem solved in " + solver.WallTime() + " milliseconds");
Console.WriteLine("Problem solved in " + solver.Iterations() + " iterations");
Console.WriteLine("Problem solved in " + solver.Nodes() + " branch-and-bound nodes");
}
}Сравнение линейной и целочисленной оптимизации
Давайте сравним решение задачи целочисленной оптимизации, показанное выше, с решением соответствующей задачи линейной оптимизации, в которой целочисленные ограничения удалены. Вы можете догадаться, что решением целочисленной задачи будет целочисленная точка в допустимой области, ближайшая к линейному решению, а именно точка x = 0 , y = 2 . Но, как вы увидите далее, это не так.
Вы можете легко изменить программу из предыдущего раздела для решения линейной задачи, внеся следующие изменения:
- Замените решатель MIP с решателем LP
Питон
# Create the mip solver with the SCIP backend. solver = pywraplp.Solver.CreateSolver("SAT") if not solver: returnС++
// Create the mip solver with the SCIP backend. std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("SCIP")); if (!solver) { LOG(WARNING) << "SCIP solver unavailable."; return; }Джава
// Create the linear solver with the SCIP backend. MPSolver solver = MPSolver.createSolver("SCIP"); if (solver == null) { System.out.println("Could not create solver SCIP"); return; }С#
// Create the linear solver with the SCIP backend. Solver solver = Solver.CreateSolver("SCIP"); if (solver is null) { return; }Питон
# Create the linear solver with the GLOP backend. solver = pywraplp.Solver.CreateSolver("GLOP") if not solver: returnС++
// Create the linear solver with the GLOP backend. std::unique_ptr<MPSolver> solver(MPSolver::CreateSolver("GLOP"));Джава
// Create the linear solver with the GLOP backend. MPSolver solver = MPSolver.createSolver("GLOP"); if (solver == null) { System.out.println("Could not create solver SCIP"); return; }С#
// Create the linear solver with the GLOP backend. Solver solver = Solver.CreateSolver("GLOP"); if (solver is null) { return; } - Замените целочисленные переменные с непрерывными переменными
Питон
infinity = solver.infinity() # x and y are integer non-negative variables. x = solver.IntVar(0.0, infinity, "x") y = solver.IntVar(0.0, infinity, "y") print("Number of variables =", solver.NumVariables())С++
const double infinity = solver->infinity(); // x and y are integer non-negative variables. MPVariable* const x = solver->MakeIntVar(0.0, infinity, "x"); MPVariable* const y = solver->MakeIntVar(0.0, infinity, "y"); LOG(INFO) << "Number of variables = " << solver->NumVariables();
Джава
double infinity = java.lang.Double.POSITIVE_INFINITY; // x and y are integer non-negative variables. MPVariable x = solver.makeIntVar(0.0, infinity, "x"); MPVariable y = solver.makeIntVar(0.0, infinity, "y"); System.out.println("Number of variables = " + solver.numVariables());С#
// x and y are integer non-negative variables. Variable x = solver.MakeIntVar(0.0, double.PositiveInfinity, "x"); Variable y = solver.MakeIntVar(0.0, double.PositiveInfinity, "y"); Console.WriteLine("Number of variables = " + solver.NumVariables());Питон
infinity = solver.infinity() # Create the variables x and y. x = solver.NumVar(0.0, infinity, "x") y = solver.NumVar(0.0, infinity, "y") print("Number of variables =", solver.NumVariables())С++
const double infinity = solver->infinity(); // Create the variables x and y. MPVariable* const x = solver->MakeNumVar(0.0, infinity, "x"); MPVariable* const y = solver->MakeNumVar(0.0, infinity, "y"); LOG(INFO) << "Number of variables = " << solver->NumVariables();
Джава
double infinity = java.lang.Double.POSITIVE_INFINITY; // Create the variables x and y. MPVariable x = solver.makeNumVar(0.0, infinity, "x"); MPVariable y = solver.makeNumVar(0.0, infinity, "y"); System.out.println("Number of variables = " + solver.numVariables());С#
// Create the variables x and y. Variable x = solver.MakeNumVar(0.0, double.PositiveInfinity, "x"); Variable y = solver.MakeNumVar(0.0, double.PositiveInfinity, "y"); Console.WriteLine("Number of variables = " + solver.NumVariables());
После внесения этих изменений и повторного запуска программы вы получите следующий результат:
Number of variables = 2 Number of constraints = 2 Objective value = 25.000000 x = 0.000000 y = 2.500000
Решение линейной задачи происходит в точке x = 0 , y = 2.5 , где целевая функция равна 25. Вот график, показывающий решения как линейной, так и целочисленной задачи.
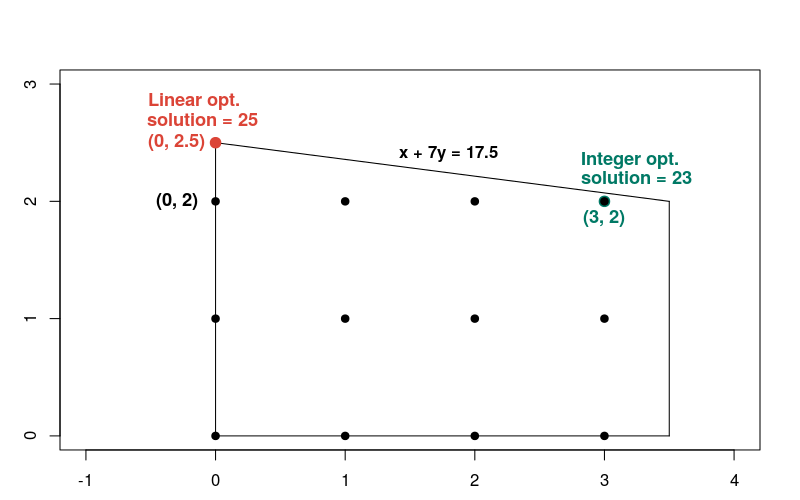
Обратите внимание, что целочисленное решение не близко к линейному решению по сравнению с большинством других целочисленных точек в допустимой области. В общем, решения задачи линейной оптимизации и соответствующих задач целочисленной оптимизации могут сильно различаться. Из-за этого два типа проблем требуют разных методов их решения.

