الاستقراء من المتّجه إلى الشبكة

تؤدي عملية الاستقراء من ملفّ رسومات متجهّة إلى ملفّ رسومات نقطية في Earth Engine إلى إنشاء Image من FeatureCollection. على وجه التحديد، يستخدم Earth Engine البيانات الرقمية المخزّنة في سمة من السمات لإجراء الاستقراء بين القيم في مواقع جغرافية جديدة خارج السمات. تؤدي عملية الاستقراء إلى إنشاء Image مستمر من القيم المستقراءة حتى المسافة المحدّدة.

التقريب المستند إلى الترجيح العكسي للمسافة

تستند دالة "معدّل التأثير العكسي للمسافة" (IDW) في Earth Engine إلى الطريقة التي وصفها باسو وآخرون (1999). تتم إضافة مَعلمة تحكّم إضافية في شكل عامل تضاؤل (gamma) على المسافة العكسية. وتشمل المَعلمات الأخرى متوسّط وانحرافًا معياريًا للسمة المطلوب إجراء الاستقراء عليها وأقصى مدى للمسافة التي سيتم الاستقراء عليها. ينشئ المثال التالي سطحًا متداخلًا ل معدّل تركيز الميثان لملء الفجوات المكانية في مجموعة البيانات الأصلية للشبكة المركّبة. يتم إنشاء FeatureCollection من خلال أخذ عيّنة من مركب الميثان لمدة أسبوعَين.

// Import two weeks of S5P methane and composite by mean.
var ch4 = ee.ImageCollection('COPERNICUS/S5P/OFFL/L3_CH4')
  .select('CH4_column_volume_mixing_ratio_dry_air')
  .filterDate('2019-08-01', '2019-08-15')
  .mean()
  .rename('ch4');

// Define an area to perform interpolation over.
var aoi =
  ee.Geometry.Polygon(
    [[[-95.68487605978851, 43.09844605027055],
       [-95.68487605978851, 37.39358590079781],
       [-87.96148738791351, 37.39358590079781],
       [-87.96148738791351, 43.09844605027055]]], null, false);

// Sample the methane composite to generate a FeatureCollection.
var samples = ch4.addBands(ee.Image.pixelLonLat())
  .sample({region: aoi, numPixels: 1500,
    scale:1000, projection: 'EPSG:4326'})
  .map(function(sample) {
    var lat = sample.get('latitude');
    var lon = sample.get('longitude');
    var ch4 = sample.get('ch4');
    return ee.Feature(ee.Geometry.Point([lon, lat]), {ch4: ch4});
  });

// Combine mean and standard deviation reducers for efficiency.
var combinedReducer = ee.Reducer.mean().combine({
  reducer2: ee.Reducer.stdDev(),
  sharedInputs: true});

// Estimate global mean and standard deviation from the points.
var stats = samples.reduceColumns({
  reducer: combinedReducer,
  selectors: ['ch4']});

// Do the interpolation, valid to 70 kilometers.
var interpolated = samples.inverseDistance({
  range: 7e4,
  propertyName: 'ch4',
  mean: stats.get('mean'),
  stdDev: stats.get('stdDev'),
  gamma: 0.3});

// Define visualization arguments.
var band_viz = {
  min: 1800,
  max: 1900,
  palette: ['0D0887', '5B02A3', '9A179B', 'CB4678',
            'EB7852', 'FBB32F', 'F0F921']};

// Display to map.
Map.centerObject(aoi, 7);
Map.addLayer(ch4, band_viz, 'CH4');
Map.addLayer(interpolated, band_viz, 'CH4 Interpolated');

يُرجى العِلم أنّه، وفقًا لما هو محدّد في المَعلمة range، لا يتم استخدام الاستقراء إلا في نطاق 70 كيلومترًا كحد أقصى من أقرب محطة قياس.

طريقة Kriging

طريقة التداخل الكريجي هي طريقة للتداخل تستخدِم تقديرًا مستنِدًا إلى نموذج لالتباين النصفي لإنشاء صورة للقيم المتداخلة التي تشكّل مزيجًا مثاليًا للقيم في المواقع الجغرافية المعروفة. يتطلّب مقدّر Kriging مَعلمات تصف شكل نصف المتغير الملائم لنقاط data المعروفة. يوضّح الشكل 1 هذه المَعلمات.

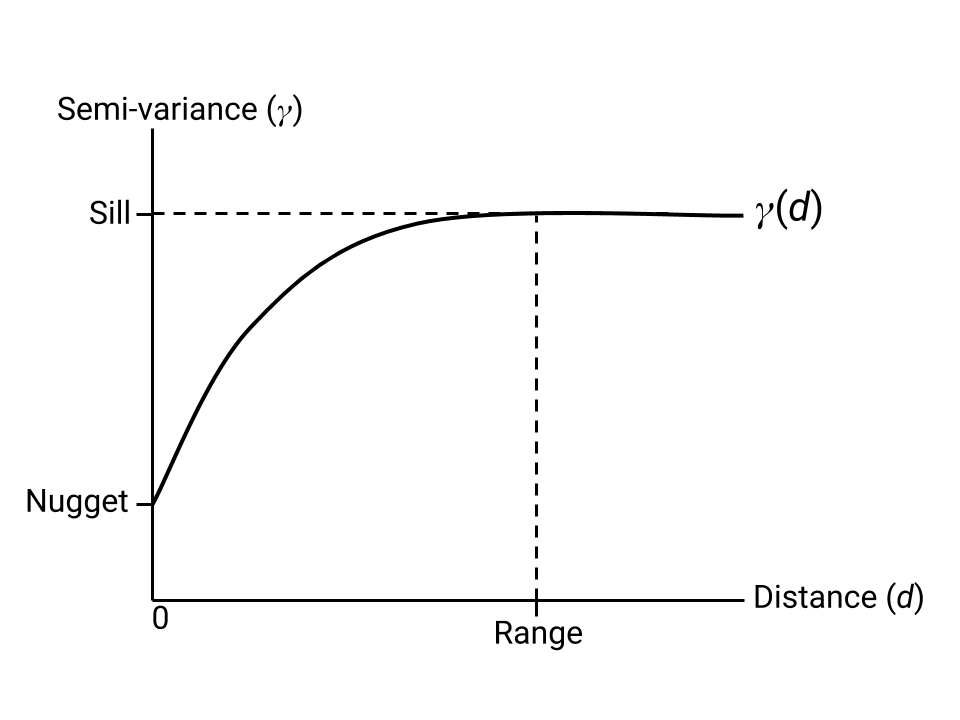
الشكل 1. مَعلمات nugget وsill وrange موضّحة في دالة متغيرة مثالية.

يأخذ المثال التالي عيّنات من صورة درجة حرارة سطح البحر (SST) في مواقع عشوائية، ثم يُحدِّد درجة حرارة سطح البحر من العيّنة باستخدام طريقة Kriging:

// Load an image of sea surface temperature (SST).
var sst = ee.Image('NOAA/AVHRR_Pathfinder_V52_L3/20120802025048')
  .select('sea_surface_temperature')
  .rename('sst')
  .divide(100);

// Define a geometry in which to sample points
var geometry = ee.Geometry.Rectangle([-65.60, 31.75, -52.18, 43.12]);

// Sample the SST image at 1000 random locations.
var samples = sst.addBands(ee.Image.pixelLonLat())
  .sample({region: geometry, numPixels: 1000})
  .map(function(sample) {
    var lat = sample.get('latitude');
    var lon = sample.get('longitude');
    var sst = sample.get('sst');
    return ee.Feature(ee.Geometry.Point([lon, lat]), {sst: sst});
  });

// Interpolate SST from the sampled points.
var interpolated = samples.kriging({
  propertyName: 'sst',
  shape: 'exponential',
  range: 100 * 1000,
  sill: 1.0,
  nugget: 0.1,
  maxDistance: 100 * 1000,
  reducer: 'mean',
});

var colors = ['00007F', '0000FF', '0074FF',
              '0DFFEA', '8CFF41', 'FFDD00',
              'FF3700', 'C30000', '790000'];
var vis = {min:-3, max:40, palette: colors};

Map.setCenter(-60.029, 36.457, 5);
Map.addLayer(interpolated, vis, 'Interpolated');
Map.addLayer(sst, vis, 'Raw SST');
Map.addLayer(samples, {}, 'Samples', false);

يتم تحديد حجم الحي الذي سيتم فيه إجراء الاستقراء بالمَعلمة maxDistance. سيؤدي استخدام أحجام أكبر إلى الحصول على نتائج أكثر سلاسة ولكن مع عمليات حسابية أبطأ.