بردار به درونیابی شطرنجی

درون یابی از بردار به شطرنجی در Earth Engine یک Image از یک FeatureCollection ایجاد می کند. به طور خاص، Earth Engine از داده های عددی ذخیره شده در ویژگی ویژگی ها برای درون یابی مقادیر در مکان های جدید خارج از ویژگی ها استفاده می کند. درون یابی منجر به یک Image پیوسته از مقادیر درونیابی شده تا فاصله مشخص می شود.

درونیابی وزنی با فاصله معکوس

تابع وزن دهی معکوس فاصله (IDW) در Earth Engine بر اساس روش توصیف شده توسط Basso و همکاران است. (1999) . یک پارامتر کنترل اضافی به شکل ضریب واپاشی ( gamma ) در فاصله معکوس اضافه می شود. پارامترهای دیگر عبارتند از میانگین و انحراف استاندارد ویژگی برای درون یابی و حداکثر فاصله بردی که باید درون یابی شود. مثال زیر یک سطح درونیابی شده از غلظت متان ایجاد می کند تا شکاف های فضایی در مجموعه داده شطرنجی اصلی را پر کند. FeatureCollection با نمونه برداری از یک کامپوزیت متان دو هفته ای تولید می شود.

// Import two weeks of S5P methane and composite by mean.
var ch4 = ee.ImageCollection('COPERNICUS/S5P/OFFL/L3_CH4')
  .select('CH4_column_volume_mixing_ratio_dry_air')
  .filterDate('2019-08-01', '2019-08-15')
  .mean()
  .rename('ch4');

// Define an area to perform interpolation over.
var aoi =
  ee.Geometry.Polygon(
    [[[-95.68487605978851, 43.09844605027055],
       [-95.68487605978851, 37.39358590079781],
       [-87.96148738791351, 37.39358590079781],
       [-87.96148738791351, 43.09844605027055]]], null, false);

// Sample the methane composite to generate a FeatureCollection.
var samples = ch4.addBands(ee.Image.pixelLonLat())
  .sample({region: aoi, numPixels: 1500,
    scale:1000, projection: 'EPSG:4326'})
  .map(function(sample) {
    var lat = sample.get('latitude');
    var lon = sample.get('longitude');
    var ch4 = sample.get('ch4');
    return ee.Feature(ee.Geometry.Point([lon, lat]), {ch4: ch4});
  });

// Combine mean and standard deviation reducers for efficiency.
var combinedReducer = ee.Reducer.mean().combine({
  reducer2: ee.Reducer.stdDev(),
  sharedInputs: true});

// Estimate global mean and standard deviation from the points.
var stats = samples.reduceColumns({
  reducer: combinedReducer,
  selectors: ['ch4']});

// Do the interpolation, valid to 70 kilometers.
var interpolated = samples.inverseDistance({
  range: 7e4,
  propertyName: 'ch4',
  mean: stats.get('mean'),
  stdDev: stats.get('stdDev'),
  gamma: 0.3});

// Define visualization arguments.
var band_viz = {
  min: 1800,
  max: 1900,
  palette: ['0D0887', '5B02A3', '9A179B', 'CB4678',
            'EB7852', 'FBB32F', 'F0F921']};

// Display to map.
Map.centerObject(aoi, 7);
Map.addLayer(ch4, band_viz, 'CH4');
Map.addLayer(interpolated, band_viz, 'CH4 Interpolated');

توجه داشته باشید که همانطور که توسط پارامتر range مشخص شده است، درون یابی فقط تا 70 کیلومتری نزدیکترین ایستگاه اندازه گیری وجود دارد.

کریجینگ

کریجینگ یک روش درون یابی است که از یک تخمین مدل شده از نیمه واریانس برای ایجاد تصویری از مقادیر درونیابی شده استفاده می کند که ترکیبی بهینه از مقادیر در مکان های شناخته شده است. تخمین‌گر کریجینگ به پارامترهایی نیاز دارد که شکل نیم‌واریوگرام متناسب با نقاط داده شناخته‌شده را توصیف می‌کنند. این پارامترها در شکل 1 نشان داده شده اند.

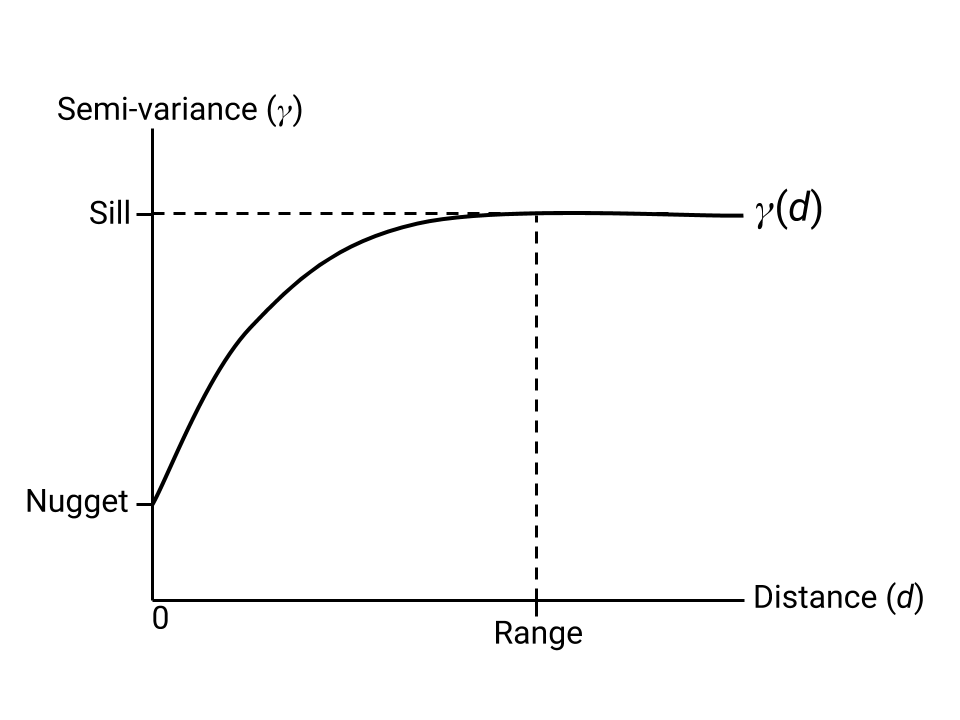
شکل 1. پارامترهای nugget ، sill و range نشان داده شده بر روی یک تابع واریوگرام ایده آل.

مثال زیر یک تصویر دمای سطح دریا (SST) را در مکان‌های تصادفی نمونه‌برداری می‌کند، سپس با استفاده از Kriging، SST را از نمونه درون‌یابی می‌کند:

// Load an image of sea surface temperature (SST).
var sst = ee.Image('NOAA/AVHRR_Pathfinder_V52_L3/20120802025048')
  .select('sea_surface_temperature')
  .rename('sst')
  .divide(100);

// Define a geometry in which to sample points
var geometry = ee.Geometry.Rectangle([-65.60, 31.75, -52.18, 43.12]);

// Sample the SST image at 1000 random locations.
var samples = sst.addBands(ee.Image.pixelLonLat())
  .sample({region: geometry, numPixels: 1000})
  .map(function(sample) {
    var lat = sample.get('latitude');
    var lon = sample.get('longitude');
    var sst = sample.get('sst');
    return ee.Feature(ee.Geometry.Point([lon, lat]), {sst: sst});
  });

// Interpolate SST from the sampled points.
var interpolated = samples.kriging({
  propertyName: 'sst',
  shape: 'exponential',
  range: 100 * 1000,
  sill: 1.0,
  nugget: 0.1,
  maxDistance: 100 * 1000,
  reducer: 'mean',
});

var colors = ['00007F', '0000FF', '0074FF',
              '0DFFEA', '8CFF41', 'FFDD00',
              'FF3700', 'C30000', '790000'];
var vis = {min:-3, max:40, palette: colors};

Map.setCenter(-60.029, 36.457, 5);
Map.addLayer(interpolated, vis, 'Interpolated');
Map.addLayer(sst, vis, 'Raw SST');
Map.addLayer(samples, {}, 'Samples', false);

اندازه همسایگی که در آن درون یابی انجام می شود با پارامتر maxDistance مشخص می شود. اندازه های بزرگتر منجر به خروجی نرم تر اما محاسبات کندتر می شود.